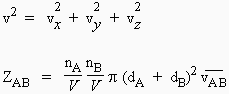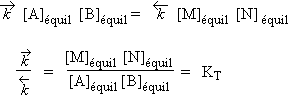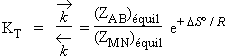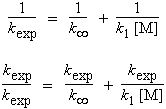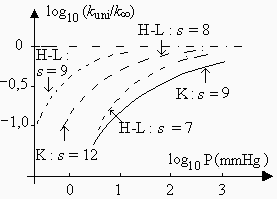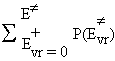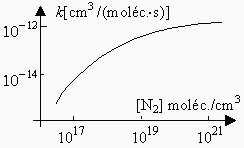CHAPITRE 2
THÉORIE DES VITESSES DE RÉACTION
|
Intuitivement le scientifique imagine, sait, ou pense que pour qu’il y ait réaction chimique entre deux entités chimiques, il faut qu’il y ait (condition nécessaire) une collision physique. Questions :
|
Objectifs spécifiques
- Connaître les grands principes qui conduisent à la théorie des collisions.
- Être capable d’appliquer l’équation d’ARRHÉNIUS.
- Comprendre pourquoi la constante de vitesse peut varier en fonction de la température.
- Comprendre l’idée de base sur laquelle se fonde la théorie du complexe activé.
- Être capable de calculer les fonctions de partition pour des molécules simples et de connaître les applications possibles de la théorie du complexe activé.
- Pouvoir appliquer l’équation d’EYRING et en déduire les conclusions sur des réactions particulières.
- Comprendre l’importance des théories sur les réactions unimoléculaires.
- Comprendre la théorie RRKM.
1. Théorie cinétique des gaz - vitesse de collision
Une condition simple (pas nécessairement juste) que deux molécules A et B réactives doivent remplir pour qu’il y ait réaction chimique est que ces molécules doivent se rencontrer physiquement. Au cours de la collision des liaisons se rompent, d’autres se reforment. Par conséquent, la vitesse de réaction chimique ne peut être plus grande que la vitesse de collisions physiques. En fait on verra qu’elle est, en général, inférieure à celle-ci. En effet, toute collision physique n’est pas nécessairement suivie d’une réaction chimique.
| 2.1 | Vitesse de réaction chimique < vitesse de collision physique |
Il est donc nécessaire de calculer la vitesse de collision physique ZAB. En phase gazeuse, les molécules sont animées de mouvement brownien et une molécule se déplace avec une vitesse
| 2.2 |
|
de telle sorte que
2.3 |
|
|
|
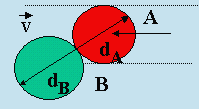
Figure 2.1. Collision entre deux particules.
Lorsque les centres des molécules A et B seront à une distance (rA + rB), il y aura collision (Fig. 2.1). Une molécule A se déplaçant dans une direction quelconque va donc rencontrer toutes les molécules se trouvant dans un cylindre déterminé par le diamètre dA de la molécule A. La théorie cinétique des gaz permet de calculer le nombre de collisions entre les molécules A et B par unité de temps (ou encore appelée la fréquence de collisions entre les molécules A et B).
NA/V et NB/V
et sont les concentrations de A et de B, [A] et [B], exprimées en nombre de molécules par
unité de volume et ![]() est la vitesse moyenne des molécules A. En fait les molécules
A et B sont en mouvement. Il faut donc parler de vitesse relative
est la vitesse moyenne des molécules A. En fait les molécules
A et B sont en mouvement. Il faut donc parler de vitesse relative
![]() . En outre, la
vitesse est liée à la température par la relation (mA et mB
sont respectivement les masses des molécules A et B) :
. En outre, la
vitesse est liée à la température par la relation (mA et mB
sont respectivement les masses des molécules A et B) :
| 2.4 |
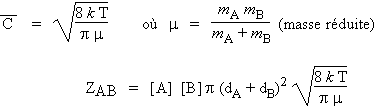 |
2.5 |
Les masses molaires, MA et MB, sont souvent plus appropriées que les masses moléculaires pour les calculs :
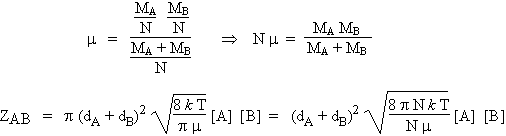
On a vu au chapitre 1 que la vitesse de réaction chimique se met sous la forme v = k [A] [B]. Cette équation combinée à la précédente montre que la constante de vitesse dépend de la racine carrée de la température, T1/2 :
![]()
Exemple
Reprenons l’exemple de la réaction en phase gazeuse entre NO et ClNO2 de l’exemple précédent pour l’équation d’ARRHÉNIUS. La distance critique de collision est estimée à 0,35 nm/molécule1/2. Les unités sont prises de façon à ce que le produit p s 2 soit en unité de surface par molécule.
|
k = (3,5 10-10)2 |
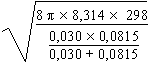 |
k = 2,1 10-16 m3 · molécule-1· s-1
k = 1,2 1014 cm3 · mol-1· s-1
Cette valeur est environ 200 fois plus grande que la valeur expérimentale calculée au chapitre 1. La raison de cette différence viendra un peu plus tard.
Si le gaz est constitué uniquement d’une molécule A réagissant avec les molécules B, la vitesse de collision de cette molécule avec les molécules B sera, AzB :
| 2.6 |
Dans le cas où le mélange gazeux n’est constitué que de molécules A, le nombre de collisions subit par une seule molécule, AzA, est tel que :
| 2.7 |
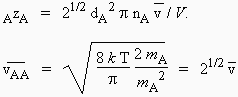 |
| En effet, |
En séparant en deux moitiés les molécules A et en appliquant 2.3, le nombre total de collisions par unité de temps est :
![]()
La théorie cinétique des gaz permet d’expliciter le libre parcours moyen l :
| 2.9 | 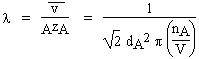 |
| On définit aussi la vitesse quadratique moyenne, |
![]()
M et m sont les grandeurs molaire et moléculaire. La définition de la vitesse moyenne telle qu’apparaissant en 2.4 implique que
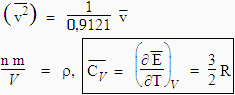 |
|
| Rappels : |
Cette relation n’est bien sûr valable que dans le cas des gaz monoatomiques qui, à la température normale, ne peuvent emmagasiner que de l’énergie de translation. Ainsi, les capacités calorifiques molaires à volume constant de l’hélium, de l’argon et du mercure sont respectivement 12,55, 12,59 et 12,47 J·mol-1·K-1.
2. Comparaison avec la réalité
Dans la réaction de décomposition de l’iodure d’hydrogène, 2 HI ® H2 + I2, en appliquant les formules indiquées plus haut (dA @ dB @ 0,2 nm à T = 667 K), on trouve une valeur de la vitesse de collision égale à 0,11 1010 [HI]2 alors que la vitesse mesurée est de 2,6 10-4 [HI]2 cm3/(molécule · s). On voit donc que la vitesse de collision physique est environ 1013 fois plus grande que la vitesse de réaction chimique. En fait, 1 collision dans 4 1012 est efficace !
On l’a vu également dans la réaction
NO + ClNO2 ® NO2 + ClNO.
La constante de vitesse de réaction chimique était environ 200 fois plus faible que celle de la vitesse de collision.
3. Les collisions efficaces
Cette notion a été introduite par ARRHÉNIUS : seules les collisions mettant en jeu une énergie cinétique de collision,
1/2 mv2 ³ Ec
peuvent se transformer en une réaction chimique. On admet que pour passer par-dessus la barrière de potentiel, la molécule doit trouver dans l’énergie de collision l’énergie critique, Ec, suffisante. Il faut donc évaluer la proportion de collisions qui développent une telle énergie. Cette probabilité de trouver une collision qui met en jeu une énergie supérieure ou égale à l’énergie critique de la réaction est donnée par le terme de BOLTZMANN : e-Ec/RT. Il s’ensuit que :
|
2.11 |
|
Tableau 2.1. Comparaison entre les vitesses mesurées et calculées à l’aide de 2.11
|
Exemples de réaction |
phase | T (K) |
vmes/vcalculée |
||
| A | 2 NOCl | ® 2 NO• + Cl2 | gaz | 700 | 1 |
| j-CH2ONa + C3H7I | ® j-CH2OC3H7 + NaI | liquide | 300 | 1 | |
| j-Br + •OH | ® j-OH + Br• | liquide | 310 | 1,1 | |
| p-CH3-j-N2Cl + •OH | ® produits | liquide | 333 | 0,94 | |
| B | 2 HI | ® H2 + I2 | gaz | 660 | 0,5 |
| H2 + I2 | ® 2 HI | gaz | 660 | 0,5 | |
| C | 2 NO2 | ® 2 NO• + O2 | gaz | 610 | 6 10-2 |
| 2 CF2=CF2 | ® (CF2)4 | gaz | 700 | 8 10-4 | |
| C2H4 + C4H8 | ® cyclo-C6H10 | gaz | 750 |
4 10-5 |
|
Partie A du tableau : l’accord
est presque exemplaire.
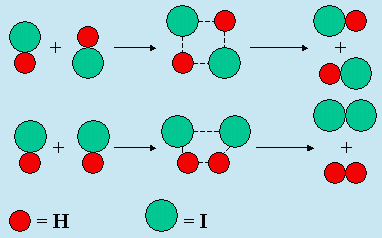
Partie B du tableau : l’accord est à peine moins bon en ce qui regarde les réactions
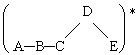
impliquant HI. On peut cependant expliquer facilement le facteur 1/2. En effet,
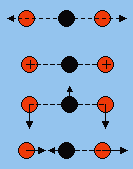
l’orientation relative des deux molécules réactives donne, une fois sur deux, la bonne
paire de produits : Fig. 2.2.
|
|
Figure 2.2. Effet de l’orientation relative des réactifs pendant une collision.
Autre exemple :
Na• + CH3CH2CH2CH2Cl ® NaCl + n-C4H9•
Il faut bien entendu que la collision de l’atome de sodium se fasse sur la bonne extrémité de la molécule de chlorure de n-butyle. On doit donc introduire un facteur de correction, P, inférieur à l’unité. Ce facteur est appelé le facteur stérique. Dans le cas de la décomposition thermique de l’iodure d’hydrogène, ce facteur stérique est évidemment égal à une demi. Dans la majorité des cas, ce facteur est loin d’être évident : partie C du tableau. Dans ces cas on voit que le facteur stérique pourrait être beaucoup plus petit que l’unité, ce qui est difficile à comprendre pour le moment.
|
2.12 |
|
|
avec ZAB = |
Par comparaison avec l’équation d’ARRHÉNIUS, kT = A e- Ea/RT (équation 1.9)
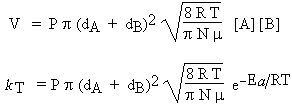 |
|
|
et |
La dépendance thermique sur le facteur pré-exponentiel est donc de T1/2. À partir de ces équations, on voit que si l’on trace la courbe Ln(k/T1/2) en fonction de 1/T, on obtiendra une droite dont la pente donnera accès à la connaissance de l’énergie d’activation.
|
Ln(k/T1/2) = P p (dA + dB)2 |
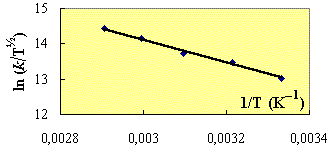
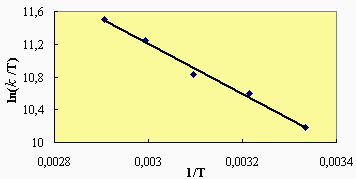
De sorte que si on applique cette équation aux données expérimentales de la réaction entre le NO et le ClNO2 (Fig. 2.3).
La valeur de l’énergie d’activation devient Ea = 26,74 kJ·mol-1 comparativement à Ea = 28,1 kJ·mol-1 . De son côté, le facteur pré exponentiel A = 3,6 1011 cm3·mol-1·s-1 comparativement à A = 6,1 1011 cm3 · mol-1·s-1. Les écarts, sans être importants, sont cependant significatifs.
|
|
Figure 2.3. Réaction entre le NO et le ClNO2 : variation de la constante du rapport k/T1/2 avec 1/T.
La théorie des collisions n’a un succès
que modéré du fait qu’il n’y a pas de modélisation du facteur stérique.
La valeur de P devrait se situer entre 0 et 1, mais il existe plusieurs cas où
sa valeur est beaucoup plus grande que 1. Cela est dû au fait que le modèle
des sphères rigides utilisé ne tient pas compte des interactions moléculaires
(attraction-répulsion) entre les molécules. Toutes les tentatives de justifier
le facteur stérique conduisent à une augmentation des paramètres qui
demeurent ajustables eux aussi.
Malgré ces faiblesses la théorie des collisions permet de jeter les bases sur
les paramètres affectant les vitesses des réactions. On y voit entre autre que
la température joue un rôle au niveau de l’énergie des collisions mais
aussi un rôle dans la fréquence des collisions.
4. L’entropie de la réaction
Soit la réaction
A + B
![]() M + N
M + N
Les vitesses des réactions directe et inverse s’expriment sous les formes :
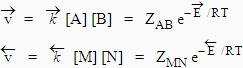
À l’équilibre, les vitesses de réactions de droite vers la gauche et de gauche vers la droite sont égales.
![]()
|
2.14 |
|
Mais l’équilibre:
![]()
| 2.15 |
|
= e- DH / RT |
|
|
La constante thermodynamique KT = e-DGº/RT = e-DH º/RT. e+DS º/R
car DG = DH - TDS
et puisque
![]()
| 2.16 |
|
Dans la théorie des collisions moléculaires,
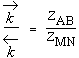
Cela correspond à une variation d'entropie nulle. Or cela est loin d'être toujours le cas. Il faut donc corriger l'équation 2.16 par un terme tenant compte de la variation d’entropie au cours de la réaction.
| 2.17 |
Vitesse de réaction £ vitesse de collision ´ e-Ec/RT ´ P ´ e+DSº/R |
5. La théorie du complexe activé
La théorie des collisions ne fait intervenir que l’énergie cinétique libérée dans la collision physique pour permettre à la molécule de passer par dessus la barrière de potentiel, pour vaincre l’énergie d’activation. Or si l’on pense que, par exemple, l’énergie vibrationnelle de la liaison qui est coupée dans l’acte primaire, puisqu’il existe un couplage entre les différents modes de vibration, pourquoi ne pourrait-on pas inclure l’énergie disponible dans ce réseau de vibration. Pourquoi aussi ne pourrait-on pas tenir compte de l’énergie de rotation. La question devient donc : comment faire intervenir ces énergies de rotation et de vibration dans un formalisme mathématique.
Plusieurs grands noms de physico-chimistes ont été intimement liés au progrès de la théorie du complexe activé. Citons LONDON (1928), KASSEL (1932), EYRING (1931), HINSHELWOOD (1935), NOYES (1925-1939), ...
Principe et description :
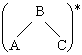
Soit la réaction
A + B ![]() ( A - B )* ® C + D
( A - B )* ® C + D
Admettons aussi que la réaction inverse, C + D ® ( A - B )* soit possible bien que quantitativement peu probable à cause de la hauteur de barrière de potentiel et de l’absence de produits C et D en début de réaction. Le principe du calcul de la vitesse de réaction revient à calculer comment varie l’énergie potentielle du système comprenant atomes et électrons,... C’est bien sûr très compliqué. Soit un cas simple :
|
A + B-C |
|
(A-B-C)* |
|
A-B + C |
|
Par exemple : Na + CH3I |
|
(Na- -I- -CH3)* ® Na I + CH3 |
||
|
ou encore : H + D-D |
|
(H- -D- -D)* ® H-D + D |
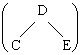
Considérons le groupe méthyle par un point et supposons que le complexe activé soit linéaire (Fig. 2.4).
|
|
Figure 2.4. Représentation d’une molécule triatomique linéaire.
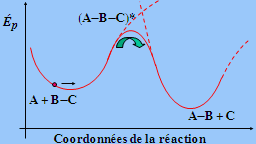
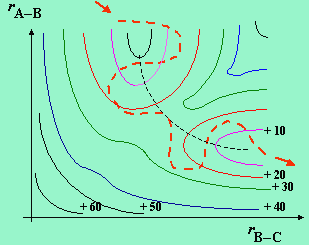
Cela revient à calculer le passage du col (Fig. 2.5 et 2.6).
|
|
Figure 2.5a. Énergie du complexe activé en fonction
des coordonnées de la réaction.
Note : l’axe des coordonnées de la réaction correspond à la ligne de
minimum des figures 2.5b et 2.5c.
|
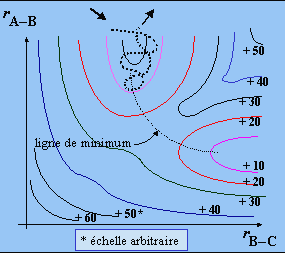
|
Figure 2.5b. Trajectoires du complexe activé
sur la surface de potentiel.
Énergie d’activation insuffisante (passage avorté) : Ea <
Ec.
|
|
Figure 2.5c. Trajectoires du complexe activé
sur la surface de potentiel.
Énergie d’activation insuffisante (passage réussi) : Ea
> Ec.
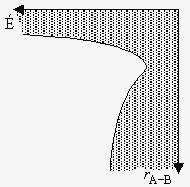 |
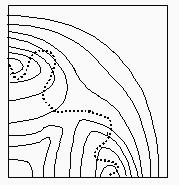 |
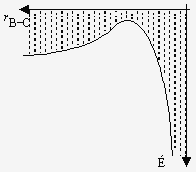 |
|
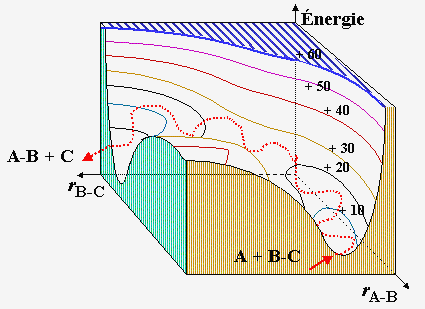
| Figures 2.6a,b,c. Représentations de la surface de potentiel en deux dimensions. | |
|
|
Figure 2.6d. Représentation de la surface de
potentiel en trois dimensions :
passage du col.
|
La réaction A + B-C |
|
(A-B-C)* est un équilibre thermodynamique : |
|
K* = |
et [(A-B-C)*] = K* [A] [B-C].
Par ailleurs supposons que la réaction (A-B-C)* ® A-B + C est une réaction élémentaire, donc d’ordre 1. La vitesse de cette réaction peut être mise sous la forme
d(produits)/dt = V(A-B) = no [(A-B-C)*] = no K* [A] [B-C].
Dans cette expression no est une fréquence : c’est la fréquence de vibration de la liaison critique, celle impliquée dans la scission du complexe activé. Il est difficile d’évaluer la concentration du complexe activé, mais la constante d’équilibre peut être formulée en termes des fonctions de partition (pour la définition et les propriétés de la fonction de partition voir un cours de mécanique statistique approprié). Les fonctions de partition sont relatives aux mouvements, donc aux énergies, de translation, de rotation, de vibration et aux niveaux électroniques des atomes, des molécules et par extension aux complexe activé (Pour plus d’informations sur les fonctions de partition, voir le cours "Chimie théorique", chapitre 11). Ces fonctions sont dénommées ftransl, frot, fvibr et félectr. Ce sont des nombres sans unités.
Selon cette approche,
![]()
Les grandeurs f sont les fonctions de partition des espèces et DEo la variation d’énergie interne à 0 K, soit la valeur d’énergie correspondant à l’énergie de vibration minimale des oscillateurs à 0 K. La fonction de partition du complexe activé peut être reformulée en terme d’une fonction de partition particulière de vibration (fvibr(B-C)) multipliée par la fonction de partition totale du complexe activé qui ne contient pas la contribution de la vibration particulière, f '*. En effet, lors de la décomposition du complexe activé, la vibration de liaison directement impliquée dans la réaction jouit d’une position particulière : elle est directement mobilisée dans le mécanisme de réaction, dans le présent exemple, fvibr(B-C).
f* = f '* ´ fvibr(B-C).
La fonction de partition particulière de la liaison en cause est telle que
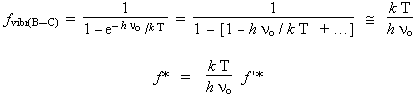
La constante thermodynamique devient :
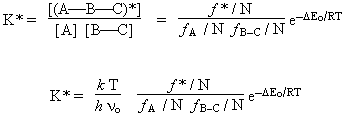 |
|
| 2.17 |
D’après ce qui a été dit plus haut, la constante de vitesse est égale au produit no K*.
| 2.18 |
Le terme entre crochet est sans unité et est habituellement désigné par K± et on l’écrit plutôt sous la forme e-DG± /RT de telle sorte que :
| k = no K* = (R T / N h)e-DG± /RT |
En se rappelant que DG = DH - T DS
| 2.19 | k = no K* = (R T / N h) e+DS± /R e-DH± /RT |
Cette relation est similaire à l'équation d'Eyring. En comparant cette formule à la formule d’ARRHÉNIUS, l’expression de la constante de vitesse prend la forme :
k = constante ´ T ´ e-DH± /RT
L’énergie d’activation du processus global est tel que Ea = DH± et le facteur pré-exponentiel est :
A = ( R / N h) e+DS± /R ´ T
En traçant la courbe Ln (k/T) en fonction de 1/T on obtient une droite dont la pente multipliée par la température donne la valeur de A.
| 2.20 | Þ v = e-DH± /RT e+DS± /R [A] [B-C] |
La théorie des collisions conduit à (P est le facteur stérique) (voir l’équation 2.5) :
| 2.21 |
V = P [A] [B-C] (dA + dB)2 |
|
En établissant que la vitesse de collision V est égale à la vitesse de formation du complexe activé, v, et en remplaçant le produit [A] [B-C] par sa valeur exprimée en 2-20, il vient que :
![]()
Si Ec = DH*, en remplaçant le produit [A] [B-C] par sa valeur exprimée en 2-20 :
| 2.22 |
|
P est donc fonction de l’entropie du complexe activé, ou mieux de la variation de l’entropie entre les réactifs A + B-C et A-B-C*. Il faut donc évaluer l’entropie du complexe activé! Ce n’est pas toujours simple (voir le cours de chimie théorique). Dans le cas des réactions mononucléaires,
A Û A*, DS* = 0 et k @ 1013 s-1 aux températures ordinaires.
Tableau 2.2 Exemples de réactions monomoléculaires
| Réactions d’isomérisation | log A* | E(kJ·mol-1) |
| CHNC ® CH3CN | 13,6 | 160,5 |
| cyclo-C3H6 ® propène | 15,2 | 271,7 |
| cis-CHD=CHD ® trans-CHD=CHD | 256,2 | |
| Réactions de décomposition (formation de molécules stables) | ||
| cyclo-C4H8 ® 2 C2H4 | 15,6 | 261,2 |
| C2H5-O-CH=CH ® C2H4 + CH3CHO | 11,4 | 183,1 |
| Réactions de décomposition (formation de radicaux) | ||
| C2H5Cl ® •C2H5 + •Cl | 14,6 | 254,1 |
| C2H6 ® 2 •CH3 | 17,4 | 383 |
| CH3N=NCH3 ® 2 •CH3 + N2 | 17,2 | 232 |
5.1 Évaluation expérimentale de D S*
Selon ARRHÉNIUS, la constante k est indépendante de la température. Selon la théorie des collisions, la même constante dépend de la racine carrée de la température et selon la théorie du complexe activé, elle dépend directement de la température. Appliquons la théorie du complexe activé à la réaction :
NO + ClNO2 ® NO2 + ClNO.
|
|
Figure 2.7. Réaction entre le NO et le ClNO2: variation de la constante du rapport k/T avec 1/T.
Ce graphe montre que la réaction est gouvernée par une équation du type : k = 7,1 × 108 T e-25,4 kJ/(mol RT)
Le terme pré-exponentiel, toujours selon la théorie du complexe activé est égal à :
7,1 × 108 M-1 s-1 = A = ( R / N h) e-DS± /R
| DS± = |
k = ( R T / N h) e+ 28,1 / R e-25 400 / R T .
Il est à remarquer que cette valeur d’entropie n’est pas une valeur standard : c’est la différence d’entropie entre les réactifs et le complexe activé. La véritable valeur d’entropie nécessite l’utilisation des propriétés standards.
5.2 Comparaison entre la théorie du complexe activé et la théorie des collisions
Prenons le cas d’une réaction bimoléculaire entre deux atomes A et B : le complexe activé sera une molécule diatomique, et sa fonction de partition sera donnée par :
f* = ftransl3 frot2
En effet, cette molécule ne peut se mouvoir que dans les trois directions du trièdre trirectangle (mouvements de translation) et autour des deux axes perpendiculaires à la liaison A-B (mouvements de rotation). La seule vibration n sera responsable de la formation des produits et sera responsable du terme (R T) / N h. Les substitutions des fonctions de partition pour les mouvements de translation et de rotation dans l’équation précédente donnent :
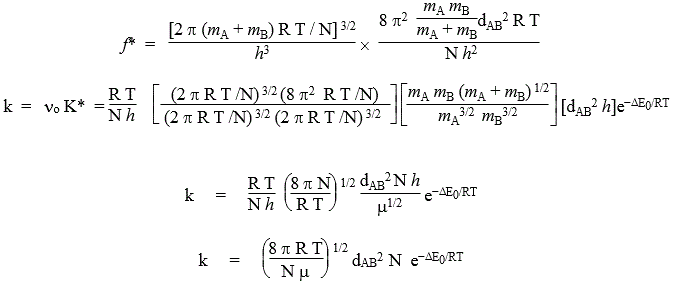
On remarque que cette dernière expression est de même forme que celle obtenue par la théorie des collisions à l’exception du nombre d’Avogadro qui transforme la constante de vitesse par mole plutôt que par molécule.
5.3 Évaluation du facteur stérique
Si on pose que toutes les molécules (réactifs et complexe activé) possèdent les mêmes valeurs de ftransl, frot et fvibr, cela permet de faire un certain nombre de simplifications sur la constante de vitesse entre deux atomes :
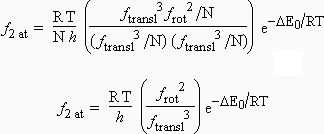
L’avantage de cette simplification est de pouvoir donner une base théorique à l’évaluation du facteur stérique. En effet, si on calcule théoriquement le ratio des constantes de vitesse : réaction type (voir tableau) sur réaction deux atomes (P = 1), cela permet de calculer le facteur stérique :
Prenons la réaction type : A + B-C ® (A-B-C)* . La valeur de k pour cette réaction est donnée par :
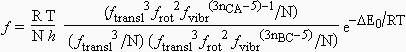
avec nCA = 3, le nombre d’atomes du complexe activé et nBC = 2 le nombre d’atomes du réactif B-C. On soustrait 1 au dénominateur pour tenir compte de la vibration responsable de la formation des produits (la liaison particulière). Si on compare cette constante k avec celle obtenue pour deux atomes :
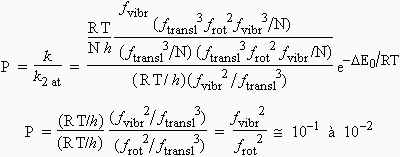
Pour différents types de complexes activés, on obtient les valeurs approximatives du facteur stérique qui apparaissent dans le tableau qui suit.
|
Type de réaction |
Rapport |
Papprox.* |
||
|
A + B- C |
® |
(A- B- C)* |
( fvibr / frot )2 |
10-2 |
|
A + B- C |
® |
|
fvibr / frot |
10-1 |
|
A- B + C- D |
® |
(A- B- C- D)* |
( fvibr / frot )4 |
10-4 |
|
A-B
+
|
® |
|
( fvibr / frot )4 |
10-4 |
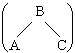 +
+
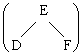 |
® |
|
( fvibr / frot )5 |
10-5 |
*: Les approximations sont basées sur des valeurs frot = 10 et fvibr = 1.
Le succès de la théorie du complexe activé, malgré les approximations apportées en fin de calcul, réside dans le fait qu’elle permet de prévoir quantitativement le facteur stérique tout au moins son ordre de grandeur.
5.4 Évaluation théorique de DS*
La théorie du complexe activé permet aussi d’évaluer le facteur pré-exponentiel et de déterminer à partir de l’équation d’Eyring (équation 2.19) la valeur de DS*. La réaction suivante a été étudiée en fonction de la température :
•Br + Cl2 ® BrCl + •Cl
Elle obéit expérimentalement à une relation du type :
k = no K* = (R T / N h ) e+ 66 ± 5 J /mol /K / R ´ e-27,1 ± 1,7 kJ (mol R T)
Si on compare ces valeurs ces valeurs aux valeurs théoriques, il faut comparer les équations 2.17 et 2.19. Cela conduit à l’expression suivante :
|
DS* = R ´ |
Cette expression théorique peut être évaluée à 300 K en calculant les fonctions de partition totale de chacun des constituants. La fonction de partition totale pour l’atome de brome :
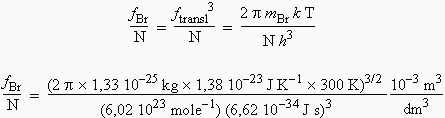
fBr / N = 1,17 106 (pour 1 mol/dm3).
La fonction de partition pour la molécule de Cl2 basée sur une distance internucléaire Cl-Cl de 0,199 nm et une fréquence de vibration de 1,67 ´ 1013 s-1 :
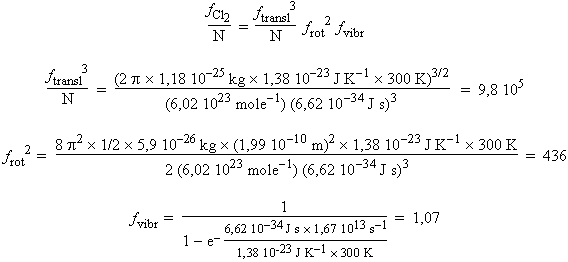
ftransl3 frot2 fvibr / N = 9,8 105 ´ 436 ´ 1,07 = 4,6 108 (pour 1 mol/dm3)
Le calcul de la fonction de partition pour le complexe activé (BrCl2) nécessite quelques approximations : on suppose premièrement que la molécule est linéaire comme la majorité des ions de type X3 . Et deuxièmement, à cause de la perte d’un électron liant, les vibrations sont plus grandes et les distances internucléaires plus élevées. Une approximation raisonnable serait de 25 % plus élevée que pour Cl2 (1,99 10-10 m) et Cl-Br (2,14 10-10 m). Le moment d’inertie est calculé pour une molécule triatomique linéaire par :
I = Si mi ri2
Dans cette équation mi est la masse de chacun des atomes i et ri la distance de l’atome i au centre de masse. La position du centre de masse est donnée par l’égalité des moments de part et d’autre du centre de masse - la somme algébrique des moments est nulle- (Fig. 2.3).
mBr ´ (2,68 10-10 - x) = mCl x + mCl ´ (2,48 10-10 + x)
x = 0,83 10-10 m
On peut maintenant calculer le moment d’inertie :
I = 1,14 10-4 kg · m2 · molécule-1.
Les valeurs de n1 et n2 (dégénérescence double)sont évaluées à 190 cm-1 et 110 cm-1. La valeur de n3 (élongation antisymétrique) n’est pas requise car c’est la vibration conduisant à la formation des produits.
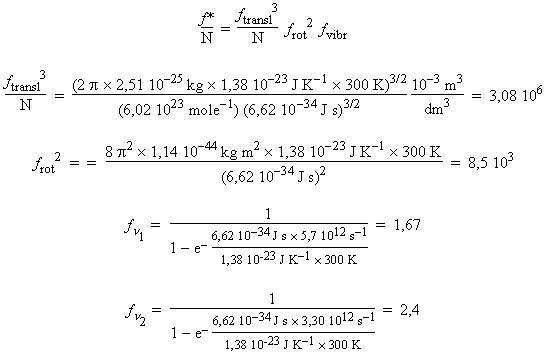
ftransl3 frot2 fvibr / N = 3,08 106 ´ 8,5 103 ´ 1,6 7 ´ 2,4 = 2,3 1011
|
DS* = 8,314 J · mol-1 · K-1 ´ |
DS* = 65 J · mol-1 · K-1
Cette valeur est très acceptable en comparaison de la valeur expérimentale de 66 ± 5 J · mole-1 · K-1. Une remarque finale : ce type de calcul est limité aux réactions en phase gazeuse car les fonctions de partition en solution ne sont généralement pas connues.
6. Les réactions quasi-monomoléculaires
- Théorie de LINDEMANN (1922)
Un certain nombre de réactions ont la particularité d’être d’ordre 1 à haute pression et d’ordre 2 à de très faibles pressions, avec une zone intermédiaire.
| [1] | M + M | ® M* + M | activation, |
| [2] | M* | ® N | réaction, |
| [3] | M* + M | ® M + M | désactivation. |
Supposons que le système réactionnaire soit en état stationnaire, de telle sorte que la concentration de l’espèce réactive soit stable :
2.23 d[M*]/dt = 0 = v1 - v2 - v3 = k1 [M]2 - k2 [M*] - k3 [M*] [M]
Þ k1 [M]2 = k2[M*] + k3 [M*] [M]
où
![]()
En outre, la vitesse de formation de N est telle que :
| 2.24 |
|
- Lorsque la pression P est grande, ou mieux lorsque k3 [M] >> k2
| 2.25 |
|
et la réaction est d’ordre 1 |
- Lorsque P est petit, ou mieux lorsque k3 [M] << k2,
| 2.26 |
|
et la réaction est d’ordre 2 |
Expérimentalement, on observe qu’en dessous d’une pression Pd et d’une certaine température Td, l’ordre tend vers 2 :
Tableau 2.3. Réactions de décomposition thermique
| Molécules | Pd (Torr) | Td(ºC) |
| N2O5 | 0,06 | 308 |
| (CH3)O | 350 | 700 |
| (C2H5)O | 150 | 700 |
| CH3N=NCH3 | 40 | 560 |
| cyclo-(CH2CH2-O-) | 285 | 617 |
| CH3CHO | 30 | 700 |
| CH3NH2 | 50 | 500 |
Ce mécanisme sous-entend que le temps de vie de l’espèce intermédiaire n’est pas infiniment court. En fait, on suppose que la molécule M* a accumulé, dans son réseau de vibration, l’énergie libérée dans la collision. Il faut admettre dès lors, que cette énergie a besoin de temps pour circuler dans ce réseau vibrationnel avant d’atteindre la bonne liaison qui doit se rompre, la bonne configuration, pour entraîner la réaction. Autrement dit, il y a lieu de différencier entre la molécule activée et l’état de transition.
- Lorsque P est quelconque, ou mieux lorsque k3 [M] @ k2
| 2.27 |
Exprimons cette vitesse sous la forme d’une réaction monomoléculaire affublée d’une constante expérimentale : kexp.
| 2.28
ou encore |
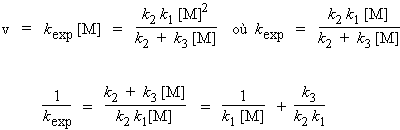
|
À haute pression, (P ® ¥), le rapport 1/kc [M] tend vers zéro ([M] tend vers l’infini) et la limite de la constante d’ordre 1 sera : k¥ = k2 k1 / k3.
|
il vient alors : |
|
En multipliant chaque
membre par kexp,
|
2.29 |
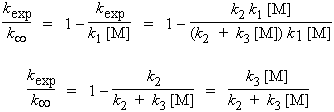 |
|
Cas particulier : kexp/k¥ = 1/2
Dans ce cas, k2 = k3 [M] ou encore, [M] = k2/k3
En unité de pression : P1/2 = k2/k3
| En se rappelant que : k2/k3 = k¥ / k1 Þ |
P1/2 = k¥ / k1 |
|
|
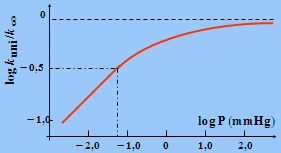
Figure 2.8. Variation du rapport log
(kuni/k¥
)
en
fonction du log P (Torr) dans
le cas de l’isomérisation du cyclopropane en propène.
La théorie de LINDEMANN rend donc bien compte du comportement des réactions d’ordre 1 à haute pression qui deviennent d’ordre 2 à basse pression. Et il y a de nombreux exemples (voir la littérature). Mais, il y a un mais! En effet, si l’on calcule la valeur de k1 à l’aide de la théorie cinétique, on doit obtenir le rapport k¥ /k1 ainsi que la détermination de P1/2. Il se trouve que, calculée ainsi, la pression P1/2 se trouve à une pression beaucoup plus haute que celle observée réellement.
Par exemple,
cis-2-butène
® trans-2-butène,
k1 = Z1 e-Eo/RT
Avec dA = 0,5 nm et Eo = 62,8 kcal·mol-1, on
trouve : k¥ = 1,9 10-5 s-1
à 469 °C
La pression calculée P1/2 est de 9 106 Torr alors qu’expérimentalement, on trouve 0,04 mmHg !
b- La correction d’HINSHELWOOD (1927)
La théorie précédente, la correction de BOLTZMANN, ne tient compte que de l’énergie échangée selon la ligne de centre de la collision. HINSHELWOOD y ajoute l’énergie vibrationnelle déjà accumulée ou en cours d’accumulation dans le réseau vibrationnel. La probabilité, qu’a la molécule activée, de passer par dessus la barrière de potentiel s’accroît puisque l’énergie vibrationnelle peut être échangée dans la collision. Il en résulte que la probabilité, PE, de passage de la barrière n’est pas liée au seul facteur de BOLTZMANN. Elle doit donc être corrigée par un facteur qui tient compte des vibrations de la molécule :
| 2.30 |
|
Dans cette équation " s " est le nombre de degrés de liberté de vibration qui participent à la réaction, ou qui peuvent accumuler de l’énergie pour les fins de la réaction.
![]()
et comme : Z3 = Z1
|
2.31 |
|
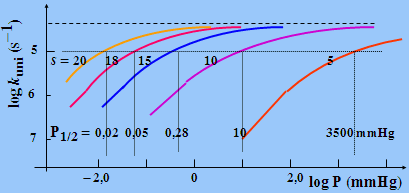 |
Figure 2.9. Isomérisation de cis-2-butène.
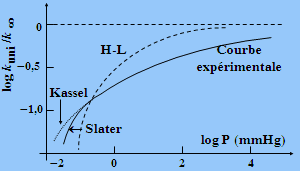
Les deux valeurs k1 et k¥ sont les deux équations de base de la théorie de HINSHELWOOD-LINDEMANN (H.-L.). Cette théorie laisse une variable un peu dans le vague. En effet, elle n’indique pas quelle est la valeur du nombre " s ". Dans le cas de l’isomérisation du cis-2-butène à 469 °C (Fig. 2.9), on montre que pour une valeur " s " = 18 on obtient une bonne concordance entre les valeurs expérimentale et calculée de P1/2. Rappelons que dans cette molécule il y a 30 degrés de liberté de vibration (3 n - 6).
Tableau 2.4. Autres exemples de réactions thermiques
| Réaction : |
s |
3n - 6 | |
| N2O | ® N2 + 1/2 O2 | 2 | 4 (*) |
| N2O5 | ® NO3 + N O2 | 7 | 15 |
| cyclo-C3H6 | ® CH3-C=CH2 | 7 | 21 |
| C2H5Cl | ® C2H4 + HCl | 8 | 18 |
| (*) : En fait 3n-5 pour une molécule linéaire. | |||
|
|
vibration longitudinale : élongation symétrique | n1 = 1 337 cm-1 |
| vibration de déformation hors plan | n2 = 667 cm-1 | |
| vibration de déformation hors plan | n2 = 667 cm-1 | |
| vibration anti symétrique | n3 = 2 349 cm-1 |
Figure 2.10. Modes de déformation de vibration du bioxyde de carbone.
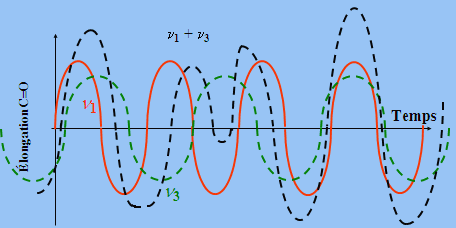
Cette molécule peut éventuellement se décomposer en oxyde de carbone et en oxygène moléculaire. Cette réaction réclame la scission d’une liaison C=O. Ce mécanisme, on l’imagine assez facilement, réclame la mise en jeu, de façon coordonnée, des deux modes d’élongation symétrique et anti-symétrique (Fig. 2.11). Dans ce cas la valeur de s serait de 2 comparativement à un nombre total de vibration qui est égal à 4.
|
|
Figure 2.11. Évolution temporelle de la longueur de la liaison.
Cette théorie de H.-L. n’est cependant pas convenable. Tout d’abord, on sait qu’en général l’énergie peut facilement passer d’un mode de vibration à un autre à l’intérieur de la molécule. Par conséquent, on ne voit pas très bien pourquoi seulement une fraction des degrés de liberté de vibration serait mis en cause. D’autre part, la courbe log kuni en fonction de la pression ne correspond pas tout à fait à la courbe expérimentale.
c- La théorie RRK (1928)
Cette théorie a été développée par RICE et RAMSPERGER d’une part et part KASSEL d’autre part. La théorie H.-L. suppose que kuni est constante quelle que soit l’énergie interne de M* pourvu, bien sûr, que l’énergie interne soit supérieure à l’énergie critique, Eint > Ec. On peut imaginer au contraire que la probabilité de trouver la bonne énergie dans la bonne liaison croît avec l’énergie totale de la molécule. D’une autre façon, la probabilité de trouver la configuration favorable à la réaction croît avec l’énergie interne. C’est l’hypothèse de la théorie RRK Cette probabilité intervient par le facteur
|
2.32 |
Si, bien sûr, E >> Ec , le facteur précédent tend vers l’unité. Cela revient à dire que toutes les molécules activées à très haute énergie sont dans l’état critique.
Cette théorie est toutefois insatisfaisante bien que meilleure que les précédentes: Fig. 2.12. Tout d’abord l’utilisation d’environ la moitié des degrés de liberté de vibration de la molécule ne repose sur aucune base logique puisque l’on sait que l’énergie "glisse" d’un degré de liberté vers les autres de façon à peu près libre. En outre, à très basse pression on n’obtient pas nécessairement un accord quantitatif entre les valeurs mesurées et calculées du rapport kuni/k¥ : Fig. 2.13.
KASSEL a introduit une amélioration à cette théorie appelée classique. En effet, il y a introduit les premiers éléments d’une approche quantifiée. Son approche admet qu’il y a toujours " s " degrés de liberté actifs. Chacun de ces degrés de liberté peut accumuler des quanta d’énergie hn identiques.
|
|
Figure 2.12. Décomposition thermique de l’azométhane Comparaison entre les expériences de RAMSPERGER (•) et les valeurs calculées à l’aide des théories H.-L. et RRK (K).
[Robinson, P. J. et K. A. Holbrook, Unimolecular Reactions, Wiley-Interscience, p. 49 (1972)].
|
|
Figure 2.13. Isomérisation du cyclopropane
Comparaison des résultats expérimentaux avec ceux des théories H.-L., RRK et de
SLATER.
[Robinson, P. J. et
K. A. Holbrook, Unimolecular Reactions, Wiley-Interscience, p. 49 (1972)].
Une molécule peut contenir n de ces quanta et l’énergie critique, Ec, est atteinte lorsque m quanta se retrouvent dans la bonne liaison, de telle sorte que m hn = Ec. Il faut donc calculer la probabilité de retrouver m des n quanta dans le bon réservoir vibrationnel. Cette probabilité est calculable :
|
2.33 |
|
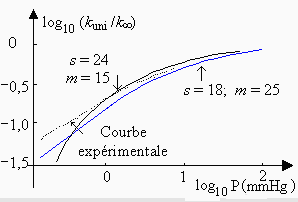
Ce facteur supplémentaire permet d’obtenir une représentation presque parfaite des résultats expérimentaux : Fig. 2.14. Cependant, cette approche n’est pas sans défaut. Le paramètre " s " est toujours ajustable. Quant au paramètre m, même si on peut le calculer, on ne peut guère le justifier. Si on connaît l’énergie critique, l’énergie moyenne des quanta de vibration est sujette à interprétation. En effet, dans une molécule, tous les niveaux de vibration sont loin d’avoir la même énergie. On a proposé d’en faire la moyenne géométrique... À la limite, en utilisant m comme un paramètre ajustable, on saura obtenir un ajustement parfait des courbes expérimentale et théorique sans pour autant leur donner une valeur scientifique exemplaire.
|
|
Figure 2.14. Isomérisation du cyclopropane Comparaison des résultats expérimentaux avec ceux des théories H.-L., RRK et de SLATER.
[ Robinson, P. J. et K. A. Holbrook, Unimolecular Reactions, Wiley-Interscience, p. 49 (1972)].
d- La théorie RRKM (1958)
MARCUS a repris le traitement R. R. K. mais cette fois de façon quantique et complète.
![]()
Par collision, une particule A acquiert de l’énergie sous forme vibrationnelle et après un certain nombre de collisions, dépendant de la pression et de la température, une molécule A* est formée. Celle-ci a dans son réseau vibrationnel l’énergie interne suffisante pour passer par-dessus la barrière de potentiel. Cependant, elle n’a pas la configuration critique requise. Il faudra un certain temps pour que cela arrive. La molécule énergétique se transforme en une molécule activée, A¹ , avec une constante de vitesse k(E¹ ). Une fois la molécule proprement activée, la réaction de formation des produits peut se produire et elle se fera avec une constante de vitesse k(E+). Le traitement complet tient compte du fait que chacune des constantes de vitesse, k(A*) et k(E+), dépend de l’énergie interne. D’autre part, cette énergie est quantifiée. Dans ces conditions,
|
2.34 |
Dans cette équation,
s et s¹ sont des facteurs statistiques qui tiennent compte de la symétrie,
h et k sont respectivement les constantes de PLANCK et de BOLTZMANN,
ƒ et ƒ¹ sont les fonctions de partition de la molécule et de la molécule activée.
Ces deux fonctions sont calculées dans le cours de chimie théorique. Ajoutons que le traitement théorique complet fait intervenir deux grandeurs fondamentales que sont :
| a-la somme des états énergétiques : |
|
P(Evr) est le nombre d’états quantifiés de vibration et de rotation dont l’énergie est inférieure ou égale à l’énergie critique.
ß- la densité d’états quantifiés, ou encore le nombre d’états par unité d’énergie : N(E).
La détermination de ƒ et de ƒ¹ demande que l’on connaisse le modèle vibrationnel complet de la molécule et de la molécule critique. Cela n’est pas toujours simple. Cependant pour des molécules ayant une vingtaine d’atomes, et à l’aide d’ordinateurs de plus en plus performants, on obtient des résultats très satisfaisants. Notons que toutes les vibrations sont introduites dans le modèle. Le paramètre " s " disparaît. Cependant, toutes les fréquences de vibration peuvent éventuellement servir de paramètres ajustables. En réalité, on a une très bonne idée des fréquences de vibration. La vibration longitudinale de la liaison C-H est entre 2 800 et 3 000 cm-1, ... Finalement, les calculs montrent que ce sont les modes de vibration qui demandent peu d’énergie qui ont une influence prépondérante sur le résultat. Ces modes sont, en effet, ceux qui accumulent le plus facilement l’énergie. En conséquence, les modes de rotation, qu’ils soient externes ou internes, ne sont pas sans conséquences : ils peuvent même être très importants. Comme on peut les intégrer dans la fonction de partition tout aussi bien que les modes de vibration, on obtient des résultats quasiment exemplaires.
Tableau 2.5. Exemples de paramètres "haute pression" de la théorie RRKM
| Réactifs | ® Produits | log A¥ (s-1) | E¥ (kJ · mol-1) |
| cyclopropane | ® propène | 15,5 | 274,2 |
| méthylcyclopropane | ® 1-butène | 14,4 | 262,5 |
| ® cis-2-butène | 14,2 | 262 | |
| ® trans-2-butène | 14,6 | 272,5 | |
| ® isobutène | 14,3 | 272 | |
| ® (total) | 14,8 | 264,2 | |
| cyclobutane | ® 2 C2H4 | 15,6 | 267,1 |
| cis-2-butène | ® trans-2-butène | 13,4 | 257,5 |
| cyclohexène | ® C2H4 + C4H8 | 15,3 | 270,6 |
| C2H5Cl | ® C2H4 + HCl | 13,2-14,6 | 236,2-254,1 |
| CH3NC | ® CH3CN | 13,6 | 160,5 |
| C2H3-O-C2H5 | ® C2H4 + CH3CHO | 11,4 | 183,1 |
| C2H5• | ® C2H4 + H• | 13,6-14,4 | 158,8-171,0 |
| etc. | |||
|
Voir : Robinson, P. J. et K. A. Holbrook, Unimolecular Reactions, Wiley-Interscience (1972). |
|||
Exemple plus détaillé d’une étude (RABINOVITCH et al., 1959-1965)
Ces auteurs ont étudié de façon systématique les réactions de décomposition du radical butyle secondaire. Pour faciliter leur étude, ils ont préparé ce radical par activation chimique, plus précisément par addition d’un atome d’hydrogène sur la double liaison d’une molécule de butène linéaire :
H• + n-C4H8 ® CH3CH2CHCH3¹ ® •CH3 + CH3CH=CH2
Le radical s-butyle ainsi formé contient une énergie interne égale à l’énergie dégagée par la réaction d’addition de l’atome d’hydrogène sur la double liaison. En faisant varier la nature des réactifs, on fait aussi varier la quantité d’énergie interne. Notons pour le moment que cette énergie est de l’ordre 40 kcal·mol-1. Le radical ainsi activé a une énergie interne suffisante pour se fragmenter puisque la formation du radical méthyle et d’une molécule de propène ne réclame que 33 kcal·mol-1 (Tableau 2.6 et Fig. 2.15).
Tableau 2.6. Réactions d’addition d’un atome d’hydrogène sur les butènes linéaires
| Réaction | EH | E | Emin+ | <E> | ka (s-1) | P (S/D) =
1/2 (en mmHg) |
|
| (kilocalories / mol) | P¥ | théorique | expérim. | ||||
| H + t-2-B | 2,0 | 38,7 | 5,7 | 8,6 | 1 107 | 0,455 | 0,55 |
| H + c-2-B | 2,0 | 40,0 | 7,0 | 9,9 | 1,5 107 | 0,68 | 0,8 |
| H + 1-B | 1,6 | 41,1 | 8,1 | 11,0 | 2,2 107 | 1,00 | 0,7 |
| D + t-2-B | 1,9 | 40,5 | 7,5 | 10,5 | 1,6 107 | 0,73 | 0,74 |
| D + c-2-B | 1,9 | 41.8 | 8,8 | 11,8 | 3,2 107 | 1,45 | 1,45 |
| D + 1-B | 1,5 | 42,9 | 9,9 | 12,9 | 4,5 107 | 2,05 | |
| t: trans; c: cis; 2-B: 2-butène; 1-B: 1-butène; Voir explication des symboles EH, Emin+ et <E> sur la figure 2.15; S/D: réaction de stabilisation/réaction de décomposition du radical butyle secondaire. | |||||||
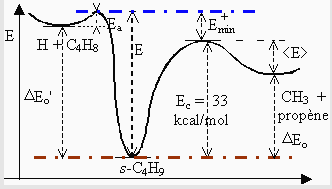 Figure 2.15. Diagramme des coordonnées réactionnelles relatif à l’étude des radicaux butyles. |
7. Le transfert d’énergie de translation
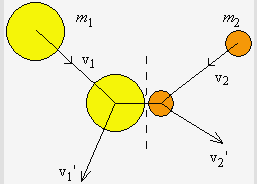
Soient deux particules de masse m1 et m2 se dirigeant l’une vers l’autre, avec une vitesse v1 et v2, et entrant en collision. On peut s’attendre à un transfert d’énergie cinétique d’une particule vers l’autre et cela tout en respectant les lois de conservation de l’énergie et de la quantité de mouvement : c’est ce que l’on appelle des collisions élastiques. Supposons que les vitesses après collisions sont v1' et v2'. On peut écrire :
m1 v1 + m2 v2 = m1 v1' + m2 v2'
et
![]()
Ces deux équations peuvent permettre de calculer les vitesses des deux particules après collisions :
|
Dans le cas où m1 º m2 on peut voir que v1' = v2 et v2' = v1. Tout se passe comme s’il y avait un échange complet d’énergie cinétique entre les deux particules. À l’autre extrême, supposons qu’une particule, m1, ait une masse beaucoup plus grande que l’autre, m1 >> m2 :
|
v1' = 2 v1 - v2 et v1' = |
La particule la plus grosse n’est pratiquement pas affectée dans son énergie cinétique, tandis que la particule la plus légère est brutalement expulsée, un peu comme une balle de ping-pong ou de tennis sur une raquette. Dans un cas ordinaire, l’énergie perdue par la particule qui a le plus d’énergie cinétique est telle que :
|
E1 - E'1 = DE1 = - DE'2 = |
En remplaçant v1' par la valeur trouvée plus haut, on peut montrer que :
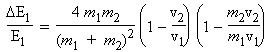
Si la particule de masse m2 est au repos par rapport à la particule incidente (v1 >> v2), on voit que la relation précédente se réduit à :
![]()
Inversement ce dernier rapport est maximum lorsque les masses m1 et m2 sont identiques. Dans ce cas, on peut conclure que le transfert d’énergie sera maximum.
8. Les collisions inélastiques
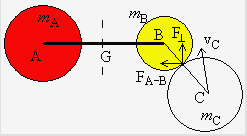
Supposons une collision entre une molécule A ¾ B de masse mA + mB et un atome C de masse mC, s’effectuant selon la ligne des centres. Si la liaison A ¾ B est rigide, la collision est élastique du type précédemment décrit. Supposons au contraire que le diamètre moléculaire, rA-B, est supérieur à la somme rA + rB, de telle sorte que les deux atomes ne sont pas liés par une liaison rigide, mais plutôt par une liaison dont la longueur peut varier sous l’influence de perturbations externes. En d’autres termes, admettons que la liaison A ¾ B est susceptible de vibrations. Dans la collision frontale A ¾ B- - -C, les règles conventionnelles s’appliquent. Une partie de l’énergie cinétique de l’atome C sera transférée dans l’énergie de translation de la molécule A ¾ B et une autre partie dans l’énergie de vibration. En effet, le ressort représentatif de la liaison A ¾ B est partiellement écrasé sous l’impact : il y a une induction d’oscillations. Le résultat est un transfert d’énergie cinétique en énergie cinétique et vibrationnelle.
Supposons maintenant que la collision présente une géométrie différente. La molécule A ¾ B et l’axe de propagation de l’atome C sont coplanaires. Il y a de plus collision selon la description de la figure 2.17. Au point de contact, l’atome C applique une force sur la molécule A ¾ B. Cette force, orientée selon la ligne des centres B¾C, peut se décomposer en deux composantes perpendiculaires. L’une est parallèle à l’axe A ¾ B, FAB, l’autre lui est perpendiculaire, F^. La première force, FAB, transforme une partie de l’énergie initiale en énergie cinétique et vibrationnelle, tout comme dans l’exemple précédent. La seconde induit un couple, un mouvement de rotation de la molécule A ¾ B autour de son centre de masse G. Une partie de l’énergie cinétique initiale est transformée en énergie de rotation.
L'étudiant verra ou a déjà vu que les niveaux de vibration et ceux de rotation sont quantifiés. L'énergie impartie dans la vibration ou dans la vibration n'est donc pas quelconque. De plus, l'énergie nécessaire pour faire "grimper" une molécule biatomique de son état de son niveau de vibration fondamental u = 0 à son premier état excité u = 1 est en général beaucoup plus importante que l'énergie disponible en translation. La conversion de l'énergie de translation en énergie de vibration est donc limitée sauf dans le cas ou l'énergie de vibration requise correspond à un mode vibrationnel actif à basse fréquence, par exemple dans le cas de molécules polyatomiques.
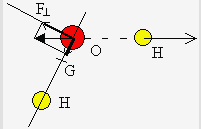
Soit enfin le cas d’une molécule d’eau au repos, photoexcitée en phase gazeuse. Considérons de plus que cette molécule, excitée suffisamment, distribue son énergie interne dans son réseau de vibration, de telle sorte que l’on puisse observer la rupture d’une liaison O ¾ H (Fig. 2.18). Au moment où la vibration d’élongation O ¾ H est suffisamment excitée, la molécule éclate et les deux atomes O et H sont propulsés sur l’axe O¾ H dans les directions opposées. Comme la molécule était au repos, elle n’avait pas de quantité de mouvement. Il s’ensuit que la quantité de mouvement généré dans l’atome d’hydrogène qui part doit être compensée par une quantité équivalente de l’atome d’oxygène (et de signe contraire). Une force est appliquée au radical OH. Cette force, qui ne passe pas par le centre de gravité du radical, peut être décomposée en deux composantes. L’une est dirigée selon l’axe O ¾ H et passe donc par le centre de masse; l’autre est perpendiculaire à cet axe et induit un mouvement de rotation. Dans ce cas, le surplus d’énergie interne, de nature vibrationnelle sert, en expulsant un atome d’hydrogène, à générer une excitation de translation, de rotation et même de vibration.
(H2O)* ® •Hcin. + •O¾Hcin., vibr., rot.
|
|
|
Figures
2.17. et 2.18. Transformations intermoléculaires d’énergie cinétique
en énergie
de translation et de
rotation avant et après collision.
On trouvera une animation simple décrivant la photodécomposition de la molécule d'eau dans la section Diaporama, Ch. 2, diapos n° 38. Un photon est absorbé par le nuage électronique de la molécule. L'énergie électronique est éventuellement transformée en énergie vibrationnelle, par exemple dans la vibration d'élongation H-O. Cette énergie si elle est suffisante pour rompre la liaison, la molécule se fragmente. Le surplus d'énergie se répartit entre l'atome d'hydrogène expulsé et le radical hydroxyle. Afin de satisfaire la loi de conservation de la quantité de mouvement, la fragmentation produit un atome d'hydrogène cinétiquement excité et un radical ·O-H qui acquiert une importante quantité d'énergie rotationnelle.
Une équipe internationale de chercheurs a mis en évidence un exemple particulier de ce type de transfert inélastique : voir Chem. & Engineering News, 86(2), 9 (2008). Dans la réaction de substitution sur l’iodure de méthyle de l’atome d’iode par un atome de chlore, le mécanisme retenu depuis longtemps implique « l’inversion du parapluie » du groupe méthyle. Cette réaction de type SN-2 est aussi connue sous le nom de la réaction ou d’inversion de WALDEN. La collision de l’atome de chlore doit se faire axialement du côté du groupe méthyle. En s’approchant de la molécule, le groupe CH3 s’inverse et l’atome d’iode est éjecté. Dans ce mécanisme, l’énergie cinétique de l’atome de chlore est partiellement utilisé sous forme d’énergie vibrationnelle (l’inversion du groupe méthyle) ce qui permet la rupture de la liaison C-I au profit de la création de la nouvelle liaison C-Cl :
Cl• + CH3I ® CH3Cl + I•
|
Cl•→
CH3I Énergie cinétique portée par l’atome de chlore |
inversion du groupe méthyle |
ClCH3
I•→ avec énergie cinétique |
Dans un système sous très haut vide, deux faisceaux croisés, l’un constitué d’ions chlorure, Cl-, l’autre de molécules d’iodure de méthyle, permettent de provoquer les collisions. En utilisant des détecteurs très particuliers, les chercheurs ont pu observer à la fois les directions privilégiées des ions I- éjectés de même que leur vitesse. Compte tenu des observations, ils ont pu en déduire que la collision n’a pas besoin d’être aussi axiale que ce que prévoit le modèle précédent. En fait, dépendamment de l’énergie cinétique des ions Cl-, la collision suit deux chemins différents. A basse énergie cinétique, le mécanisme suit celui précédemment décrit.
Par contre, à haute énergie cinétique, la collision induit tout d’abord une rotation de 360° de la molécule sur elle-même. Une fois le tour complété, la réaction d’inversion du groupe méthyle avec expulsion concomitante de l’ion iodure se produit. On constate donc que dans la collision, l’énergie cinétique de l’atome de chlore est d’abord transférée sous forme d’énergie de rotation, cette dernière est ensuite transformée en énergie de vibration, ce qui permet d’éjecter l’ion I- et d’amorcer l’inversion du groupe méthyle et ainsi de compléter la réaction de substitution.
9. Les réactions trimoléculaires
Ce n’est pas une réaction d’ordre 3, mais bien plutôt une réaction de molécularité 3, c’est-à-dire mettant en jeu une collision simultanée de trois particules : c’est un choc triple. La probabilité d’un tel choc est pratiquement nulle. On peut calculer le rapport Z3/Z2, nombre de collision de 3e ordre sur le nombre de collision de 2e ordre; ce rapport est tel que :
![]()
et à pression atmosphérique Z3/Z2 @ 10-3 à 10-4. Comme le facteur stérique est encore plus petit (orientation très particulière des réactifs) que dans le cas des réactions bimoléculaires, on doit à toutes fins pratiques ignorer ce type de réactions.
10. Les réactions thermoléculaires
Dans certains cas, il faut faire appel à des réactions impliquant la collision de trois molécules. Ces réactions sont plutôt la succession de deux réactions bimoléculaires. L’exemple précédent impliquant la formation du radical butyle secondaire chimiquement activé montre que la décomposition du radical CH3CH2CHCH3¹ n’est pas immédiate. Il faut en effet un certain temps entre le moment où l’énergie apparaît dans la nouvelle liaison C-H en cours de formation et celui où l’énergie apparaît dans la liaison C-CH3. En effet, c’est la rupture de cette liaison qui forme le radical méthyle et la molécule de propène. Si pendant ce laps de temps, intervient une collision physique, l’énergie accumulée du radical CH3CH2CHCH3¹ va être transférée vers une autre molécule. Le radical activé perd une part de son énergie interne et n’est alors plus susceptible de se décomposer. On parlera plus de réaction thermoléculaire que de réaction trimoléculaire, puisque de l’énergie interne (chaleur vibrationnelle) est échangée avec le troisième partenaire.
Note : ces réactions sont aussi appelées, réactions thermoléculaires. Le préfixe ther est sans doute plus proche du préfixe tri...
Autres exemples :
| H• + C2H4 | ® •C2H3# | ® C2H4 + H• |
| H• + H• | ® H2# (DH = - 104 kJ · mol-1) | ® H• + H• |
| Cl• + Cl• | ® Cl2# (DH = - 58 kJ · mol-1) | ® Cl• + Cl• et |
| R# + M | ® R + M |
Dans le cas de H2¹ , le temps disponible pour sa stabilisation est de l’ordre de 10-13 secondes, plus précisément c’est le temps de l’oscillation longitudinale de la vibration de la liaison H-H. Pour obtenir une seconde collision dans un temps aussi court, il faut travailler à des pressions de plusieurs milliers d’atmosphères! Dans le cas du radical butyle secondaire, le temps requis pour que l’énergie se répartisse convenablement dans le réseau vibrationnel est de l’ordre de 10-7 secondes. Dans ce cas les pressions requises pour stabiliser, refroidir la moitié des radicaux activés, sont de l’ordre du mmHg, donc très accessibles sur le plan expérimental.
|
Autre exemple : •CH3 + O2 ( + M ) |
|
CH3O2• ( + M ) |
|
|
Figure 2.19. Stabilisation de CH3O2¹ par
l’azote :
k¥
@ 2 10-12
cm3·(molécule·s)-1
en présence d’azote.
réf. : Cobos, C. J. et al., J. Phys. Chem., 89, 4332-38
(1985).
|
La collision physique nécessaire doit générer suffisamment d’énergie pour permettre au système de passer par-dessus la barrière de potentiel.
|
| 11.1 | Calculez le libre parcours moyen, la vitesse moyenne ainsi que la vitesse quadratique moyenne d’une molécule d’hydrogène, d’oxygène et de limonène dans des conditions normales TPN. |
|
Réponse : l (O2) = 0,0386 µm et la vitesse quadratique moyenne de O2 = 480 m/s. |
| 11.2 | Dans le cas de l’air sec de composition suivante : azote 79 %, oxygène 20 % et argon 1 %, calculez, sous la pression atmosphérique, le nombre de collisions par seconde dans dans un volume d’un cm3. Si cet air contient une humidité de 50 % (la pression de vapeur de l’eau à 25 °C est de 23,8 mm de mercure), calculez en la densité. |
|
Réponse : ZAB = 1,10 1020 collisions/(s cm3); D = 1,173 kg/m3. |
| 11.3 | Quelle fraction des collisions bimoléculaires à 500 °C ont une énergie cinétique relative de collision frontale supérieure à 50 kcal mol-1 ? |
|
Réponse : f = 7,33 10-15. |
| 11.4 | Dans le cas de la dimérisation du butadiène, la variation de la constante de vitesse peut être exprimée sous la forme |
| k = 9,20 10-9 e-23 690/RT cc · mol-1 · s-1 | |
| Quelle fraction du nombre total de molécules de butadiène a
l'énergie cinétique suffisante pour réagir à 300 °C, à 450 °C ? |
| 11.5 | Le diamètre moléculaire d’une molécule d’oxyde de carbone est de 3,19 10-10 m. Sous la pression de 75 kPa, calculez le nombre de collisions par seconde et par cm-3, le libre parcours moyen d’une molécule, ainsi que la distance linéaire parcourue pendant une seconde. Comparez cette distance au diamètre d’un ballon d’un litre. En déduire le nombre approximatif de collisions possibles entre une molécule de CO et les parois de ce réacteur pendant une seconde. |
| 11.6 | Dans un système expérimental, on produit des atomes d’hydrogène cinétiquement excités. Ces atomes d’hydrogène entrent en collision avec des molécules d’azote que l’on considérera au repos. Calculez l’expression théorique permettant d’évaluer la fraction de l’énergie cinétique des atomes d’hydrogène transférée aux molécules d’azote. |
| Réponse : DE1/E1 = 13,3 %. |
| 11.7 | Dans le cas d’une réaction chimique soumise à une énergie d’activation de 25 kcal·mol-1, quelle sera la fraction des collisions qui seront efficaces? Faire le même calcul avec une réaction soumise à une énergie d’activation de 410 kJ·mol-1. |
| 11.8 | Calculer à 600 K la fraction des collisions bimoléculaires pour lesquelles l'énergie de collision frontale (l'énergie associée à un degré de liberté de translation de chaque molécule) est plus grande que l'énergie d'activation (44 kcal mol-1). |
| 11.9 | Calculer à 600 K la fraction des collisions bimoléculaires pour lesquelles l'énergie d'un degré de liberté de vibration dépasse E1 dans une molécule et E2 dans l'autre molécule si |
| E1 + E2 = 44 kcal mol-1 | |
|
Réponse :
f = 9,37 10-17. |
|
| 11.11 | Calculer la fraction des collisions bimoléculaires possédant une énergie plus grande que 44 kcal mol-1 distribuée respectivement parmi 6, 12, 18 et 24 termes quadratiques d'énergie (T = 600 K). |
| 11.12 | Hinshelwood et Ashley ont obtenu les résultats suivants pour la décomposition de l'éther méthylique à 773 K (est la concentration au temps t = 0) : |
|
Trouver la constante de vitesse à haute pression et la constante de vitesse de l'étape d'activation.
| 11.13 | La constante de vitesse du premier ordre pour la décomposition du radical méthoxyméthyle, l'éther diméthylique, |
| CH3OCH3 ® CH3• + HCHO | |
| varie en fonction de la concentration d'un gaz inerte M de la façon suivante à 270 °C : |
|
k (sec-1) |
[M] (´ 106 mol · cc-1) |
|
7,83 |
0,166 |
|
9,40 |
0,286 |
|
11,8 |
0,500 |
|
13,4 |
0,770 |
Si on suppose que la théorie de Lindemann s'applique dans ce cas, estimer la constante de vitesse pour la réaction de transfert d'énergie
M + CH3OCH2• ® M + CH3OCH2•*
| 11.14 | Calculer la constante de vitesse k1 de l'étape d'activation, à 300 °C, d'une réaction monomoléculaire si l'énergie d'activation est égale à 167 kJ mol-1, si n = 12 et si |
| Z' = 1012 dm3 · mol-1 · sec-1 |
11.15 La réaction de décomposition de l’ozone gazeux se produit à travers le mécanisme suivant:
| (1) | O3 |
|
O2 + O | avec |
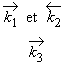 |
|
| (2) | O3 + O | ® | 2 O2 | et |
|
Établissez la réaction globale de ce
mécanisme. Si la réaction 3 est beaucoup plus lente que ce que demande l’établissement de l’équilibre thermodynamique, établissez l’équation de vitesse de la réaction globale en fonction des constantes de vitesse des étapes élémentaires et des concentrations. En déduire l’énergie d’activation du processus global en fonction des énergies d’activation de chacune des trois réactions élémentaires. |
|
Réponse : Eexp = E3 + E1 - E2. |
| 11.16 | Calculez le rapport des probabilités des collisions trimoléculaires et bimoléculaires dans un réacteur contenant de l’azote sous une pression de 1 mmHg, de 100 kPa, de 3 000 atmosphères. |
| 11.17 | La décomposition de l’acide iodhydrique en phase gazeuse s’effectue en phase homogène dans une réaction d’ordre 2 selon l’équation suivante : | ||||||||||||||||
| 2 HI (gaz) ® H2 (gaz) + I2 (gaz) | |||||||||||||||||
|
|||||||||||||||||
Cette réaction a été étudiée par BODENSTEIN à la fin du XIXe siècle entre 556 et 781 K. Dans cette région de températures, la constante de vitesse observée est telle que |
|||||||||||||||||
| A- Calculez l’énergie d’activation de cette réaction. | |||||||||||||||||
| Réponse : E = 186,61 kJ/mol. | |||||||||||||||||
| B- D’après cette donnée, déterminez selon la théorie simple des collisions la constante de vitesse de la réaction en fonction de la température et comparez le résultat avec les observations expérimentales de BODENSTEIN (Note : le diamètre moléculaire de la molécule est de 0,35 nm). | |||||||||||||||||
| Réponse : kHI(556 K) = 3,163 10-7 litre/(mole·sec). |
Pour en savoir beaucoup plus:
Robinson, P. J. et K. A. Holbrook, Unimolecular Reactions, Wiley-Interscience, New York, 1972.
Forst W., Theory of Unimolecular Reactions, Academic Press, New York, 1973; DD 501 F733.
Zewail, A. et R. B. Bernstein, Real-Time Laser Femtochemistry - Viewing the Transition from Reagents to Products, Chemical & Engineering News, 1988-11-07, pages 24-43.
Ruasse, M.-F., Approches expérimentales quantitatives de la réactivité de systèmes organiques complexes, L’Actualité chimique, septembre-octobre 1988, pages 215 ...
Sur la réaction de WALDEN (substitution de l'atome d'iode par un ion chlorure dans l'iodure de méthyle) : Chem. & Engineering News, 86(2), 9 (2008). Voir aussi la revue Science, 319, 183 (2008).
Le site de la fondation Nobel permet une navigation rapide sur divers éléments relatifs aux Prix Nobel et en particulier à leur biographie :
Sur le NET :
On ne doit pas se priver de faire des recherches sur le Net tout en maintenant un regard critique sur la qualité des sites observés. Privilégier les sites gouvernementaux, universitaires, les grandes industries, les Fondations, ...
HINSHELWOOD : http://www.almaz.com/nobel/chemistry/1956a.html (site visité le 2021-06-21).
Dernière mise à jour : 2021-07-01