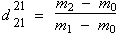
Chapitre 4
Problème Nº 1. Utilisation du pycnomètre
L’utilisation
d’un pycnomètre de volume voisin de 2 mL pour la mesure de la densité
relative d’une huile essentielle indique les mesures de pesées suivantes
obtenues à 21 °C :
1-
pycnomètre
vide, m0 : 6,066,
6,067 et 6,066 g
2-
pycnomètre
rempli d’eau distillée, m1 :
8,201, 8,200 et 8,200 g
Calculez la densité relative de l’huile essentielle ainsi que l’incertitude absolue sur la valeur résultante.
CORRIGÉ
La densité relative de l’huile essentielle par rapport à l’eau est donnée par le rapport suivant :
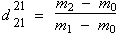
Par conséquent, compte tenu des valeurs numériques obtenues, on obtient :
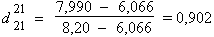
Calcul
de l’incertitude absolue
L’incertitude relative sur la mesure de la densité est donnée par la formule faisant appel aux dérivées partielles (note : dm0, dm1 et dm2 sont les variables indépendantes et représentent les incertitudes sur chacune des mesures) :
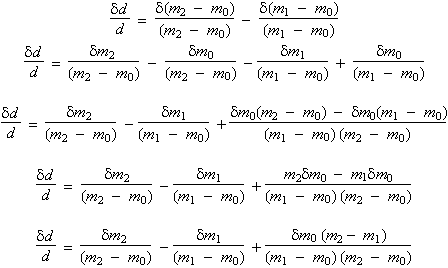
Les trois variables indépendantes sont maintenant séparées. On peut substituer les différentielles d par les incertitudes D en ne retenant que les valeurs positives :
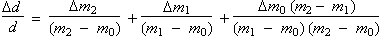
Par ailleurs, les incertitudes absolues sont les mêmes pour chacune des pesées :
Dm0
= Dm1
= Dm2
= Dm
= 0,002
g
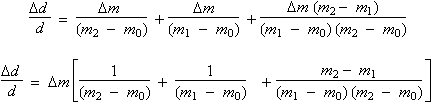
La valeur numérique de Dm est égale à 0,002 g, soit deux fois l’incertitude absolue sur la mesure de chacune pesées. En effet, il faut se rappeler que la valeur numérique de la pesée est en fait la différence entre deux mesures élémentaires, soit la mesure de la pesée elle-même et celle de la mise à zéro de la balance. Il ne reste plus qu’à remplacer les valeurs littérales par les valeurs numériques :
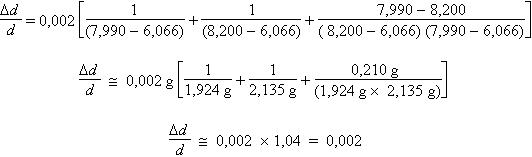
Le résultat numérique est donc entaché d’une incertitude relative de 0,2 %. La densité relative de l’huile essentielle par rapport à l’eau est donc :
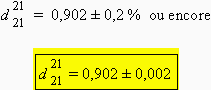
________________________________________
Problème Nº 2
Un liquide de masse volumique égale à 0,800 g cm-3 s’élève jusqu’à une hauteur de 62,5 mm dans un capillaire de 0,21 mm de diamètre. Quelle est la tension superficielle de ce liquide ? Estimer l’incertitude absolue sur ce résultat.
CORRIGÉ
a- La loi qui gouverne la tension superficielle est : s = 1/2 h (d2 – d1) g r
Dans cette relation s est la tension superficielle, h, la hauteur de liquide dans le capillaire, d2 et d1 les masses volumiques respectives du liquide et de l’air, g l’accélération de la pesanteur et r le rayon du capillaire. Dans le système CGS, on obtient :
s = 1/2 ´ 62,5 mm (0,800 g cm-3 – 0,001 2 g cm-3) ´ 981 cm s-2 ´ 0,21 mm
s = 25,72 dyne/cm
En SI, on obtient :
s
= 1/2 ´
0,0625 m (800 kg m-3 – 1,2 kg m-3)
´
9,81 m s-2
´
0,000 21 m
s = 25,72 10-5 Newton/m
b- En ignorant la densité de l’air (la masse volumique) par rapport à celle du liquide, on a :
s
= 1/2 h (d2
– d1) g r
L’incertitude
sur la valeur de la viscosité peut être obtenue à l’aide de la relation
suivante :
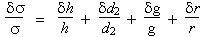
g est une constante universelle :
à ce titre on ne commet aucune erreur sur sa valeur.
Comme les mesures sont toutes indépendantes les unes des autres, on peut
transformer la relation précédente afin d’obtenir les incertitudes relatives :
![]()
| » 0,15 % + 0,125 % + 0,95 % = 1,12 % |
|
|
|
s = (25,72 ± 0,29) 10-5 Newton/m
________________________________________
Problème Nº 3
Dans un tube de rayon 0,108 ± 0,004 mm, on observe une descente capillarimétrique de 6,60 ± 0,05 cm pour le mercure. Calculez la tension de surface du mercure sachant que sa masse volumique est de 13,600 ± 0,005 g cm-3. L’angle de contact entre le mercure et le verre est nul. Faire le calcul d’erreur pour déterminer la mesure qui entraîne la plus grande incertitude, ainsi que l’incertitude expérimentale finale.
CORRIGÉ
La dénivellation capillarimétrique est donnée par la formule 4.2 puisque le cosinus de l’angle de contact est égal à l’unité :
s = (1/2) h d g r
Dans le système CGS, l’application numérique donne :
s = (1/2) × 0,0108 cm × 13,6 g cm-3 × 981 cm s-2 × 6,60 cm
s = 475 g s-2
L’incertitude sur cette mesure peut être calculée de la même manière que dans le cas qui précède :
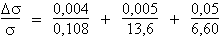
Ds
/ s
= 3,7 %
+ 0,04 %
+ 0,75 %
Ds / s = 4,49 %
L’incertitude principale vient donc de la mesure de la dénivellation puisqu’elle compte pour plus de 80 % de l’incertitude relative totale. Au total,
s = 475 ± 21 g s-2 ou encore dyne/cm
________________________________________
Problème Nº 4
a- En admettant que la tension de surface de l’eau est de 72 dyne/cm, calculez cette tension de surface en SI.
b- Si la montée de la sève dans un arbre de 30 m est explicable sur la base de la montée capillarimétrique, quel devrait être le diamètre des canaux responsable de cette montée ?
CORRIGÉ
1- Le problème N° 1 a montré la relation qui existe entre l’unité de force dans le système CGS et en SI. Pour s’en convaincre :
1 unité de force en SI º 1 kg m / s2
1 unité de force en CGS º 1 g cm / s2
De telle sorte que les rapports suivants prennent les valeurs :

2- La montée de la sève dans un arbre peut être assimilée à la montée capillarimétrique de l’eau dans un tube. La tension de surface de l’eau à 20 °C est de 72,75 dyne/cm. Par conséquent, et d’après la formule 4.2,
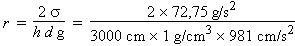
r
= 0,49
10-4
cm =
0,49 mm
Le diamètre des tubes capillaires dans un arbre de 30 m doivent donc avoir un diamètre de l’ordre du micromètre. Il faut ajouter que la sève d'un arbre n'est pas que de l'eau pure. La tension de surface de la sève peut donc être différente de celle de l'eau ...
________________________________________
Problème Nº 5
Une sphère en acier de 4,0 cm de diamètre et de 7,9 g cm-3 de masse volumique tombe de 1,00 m en 55 s dans l’huile de densité 1,1 g cm-3. Calculez la viscosité de l’huile en poises.
CORRIGÉ
La loi qui s’applique à ce type d’expérience est celle de POISEUILLE :
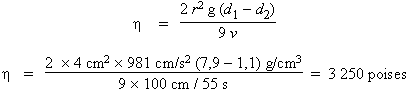
h
= 3 250 poises
L’incertitude
sur la valeur de la viscosité peut être obtenue à l’aide de la relation
suivante
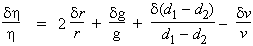
Avant
de passer aux incertitudes relatives, il y a lieu de séparer certaines
variables.
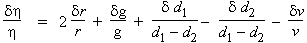
Maintenant
que les variables sont séparées, on peut établir les incertitudes relatives :
![]()
On a introduit le signe positif
partout puisque l’on ne sait pas dans quel sens les incertitudes vont
s’additionner. On ne retient que
le cas défavorable où toutes les incertitudes relatives s’ajoutent.
![]()
Quelques explications s’imposent. Le diamètre de la bille est donné 4,0 cm.
On doit donc lire 4,0 ± 0,1 cm. Le
rayon est donc de 2,0 ± 0,05 cm. L’incertitude
relative sur le rayon est donc égal à 0,05 / 2,0.
De la même manière, puisque d1 = 7,9 g
cm-3,
l’incertitude absolue sur cette valeur est de 0,1. Et ainsi de suite pour la valeur de d2.
Finalement, l’incertitude sur la vitesse doit être calculée.
Puisque u
=
d / t,
![]()
L’incertitude relative sur la tension superficielle devient :
Dh/h » 10 % + 1,5 % + 1,5 % + 3 % = 16 %
Donc,
h
= 3250
± 520 poises.
Note, si l’on veut améliorer la précision de la mesure, il faut en priorité diminuer l’incertitude relative sur la le rayon de la sphère en acier. Avec un pied à coulisse, par exemple, on sait mesurer ce type de diamètre à moins de 0,1 mm, et donc obtenir une incertitude relative 10 fois plus faible. On obtiendrait ainsi une incertitude relative de 7 %. Bien sûr, la bille doit être parfaitement sphérique…
________________________________________
Problème Nº 6
À partir de la loi de NEWTON,
![]()
Dans cette équation t est la force de glissement (tension de cisaillement), Q la surface du plan de glissement, du/dl le gradient de vitesse (variation de vitesse par unité de distance) et h la viscosité dynamique du milieu. Déterminez l’unité de h.
CORRIGÉ
________________________________________
Problème Nº 7
À 1050 K, un verre fondu a une viscosité de 1,46 105 kg m-1 s-1 et une masse volumique de 3,54 kg dm-3. Combien prendra une sphère de platine de 1 cm de diamètre pour descendre de 1 cm ?
CORRIGÉ
________________________________________
Problème Nº 8. Viscosité intrinsèque
On a mesuré la viscosité relative hr d’une solution contenant différentes concentrations C d'un polymère à 25 °C :
|
C(kg/m3) |
0,0152 |
0,0271 |
0,0541 |
|
hr |
1,226 |
1,425 |
1,983 |
Déterminez la viscosité intrinsèque du polymère.
CORRIGÉ
L’application des formules 4.14, 4.15 et 4.16 permet de compléter le tableau qui suit.
|
C(kg/m3) |
0,0152 |
0,0271 |
0,0541 |
|
hr |
1,226 |
1,425 |
1,983 |
|
hs = hr - 1 |
0,226 |
0,425 |
0,983 |
|
hs / C |
0,1487 |
0,1568 |
0,1817 |
|
Ln hr |
0,204 |
0,354 |
0,685 |
|
(Ln hr) / C |
0,1342 |
0,1307 |
0,1266 |
Le
tracé des deux courbes hs
/ C et (Ln hr)
/ C en fonction de C et leur extrapolation à concentration nulle permet
d’obtenir la viscosité intrinsèque [h]
du polymère :
|
|
|
|
L'extrapolation des droites - courbe supérieure : hs/C = f(C) et courbe inférieure : [Ln hs/C] = f(C) - produit une valeur limite moyenne de 0,1356 ± 0,001. En utilisant un polynôme d'ordre 2 pour chacune des deux courbes, on obtient une valeur moyenne de 0,1405 ± 0,0005. Dans ce dernier cas les coefficients de corrélation ne peuvent être différents de l’unité puisqu’on dispose seulement de trois points pour déterminer les coefficients de la parabole. En résumé,
[h] » Lim de hs / C » Lim de [Ln hs] / C lorsque C tend vers 0
[h]
=
0,138 ± 0,003
Unité
de cette limite : hr
est une viscosité relative (rapport
entre la viscosité de la solution et celle du solvant pur). Cette grandeur est donc sans unité. hs
est donc également sans unité.
Le rapport hs
/ C a donc l’unité de
l’unité de l’inverse d’une concentration. Ici,
[h]
s’exprime en m3/kg.
[h]
= 0,138
m3/kg
On aurait retrouvé la même expression d’unité en utilisant la valeur
limite du rapport (Ln hr)
/ C.
________________________________________
Problème Nº 9
Les diverses fractions d’un polymère
dissout à 25 °C dans un solvant
approprié, montrent les viscosités
intrinsèques suivantes :
|
M(g/mole) |
34 000 |
61
000 |
130
000 |
|
[h] |
1,02 |
1,60 |
2,75 |
Déterminez les constantes a et k pour ce couple solvant-polymère.
CORRIGÉ
[h]
= k
Ma
ou encore :
Ln
[h]
= a Ln M +
ln k
En traçant la droite Ln [h]
en fonction de Ln M, la pente à la droite est égale au coefficient a
et l’ordonnée à l’origine correspond à la valeur de Ln k.
En utilisant par exemple un outil comme Excel, on obtient :
Ln
[h]
= 0,7384 Ln M – 7,7667
Par conséquent :
a
= 0,74
et
Ln
k =
-
7,7667,
ou encore :
k
= 4,24 10-4
___________________________________
Problème Nº 10. Équation d'Antoine
À l’aide de l’équation d’ANTOINE calculez la pression barométrique
en mmHg que l’on devrait observer à La Paz.
On rappelle que l’eau bout à 83 °C.
CORRIGÉ
L’équation d’ANTOINE est donnée à la formule 4.20 (la pression P exprimée en bar : 1 bar = 750 mm de mercure et la température T est en Kelvin) :
log10
P =
A -
[B / (T + C)]
Comme on observe une diminution de la température d’ébullition, l’équation devient :
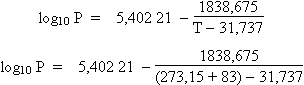
log10 P = 5,402 21 - 5,66 770 = - 0,26549
En passant au logarithme népérien, si cela est nécessaire, on obtient :
Ln P = 2,303 log10 P = 2,303 ´ - 0,26549 = - 0,611 42
P
= 0,542 bar = 407 mm de
mercure
La pression atmosphérique à La Paz est donc bien inférieure à la pression normalement rencontrée au niveau de la mer, soit 760 mmHg.
________________________________________
Problème Nº 11
En admettant que la chaleur latente de vaporisation de l’eau est de 2 257 J g-1, calculez la température à laquelle la pression de vapeur saturante de l’eau est de 2 atm.
CORRIGÉ
La relation
entre la température d’ébullition, la pression et la chaleur latente de
vaporisation est donnée par la relation de CLAPEYRON (équation 4.17) :
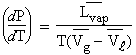
En
admettant que la vapeur se comporte comme un gaz idéal et en remarquant que le
volume molaire de l’eau liquide est beaucoup plus petit que celui de l’eau
vapeur, cette formule peut être simplifiée de telle sorte qu, le produit PV étant
égal à n RT, on obtient :
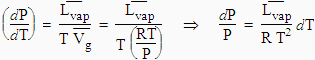
En intégrant cette dernière relation, on obtient l’équation 4.18 :
![]()
L’application numérique de cette relation entre deux pressions différentes donne :
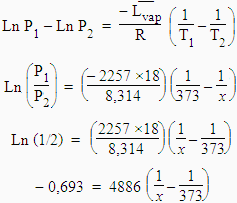
x
= 393,8 K
= 120,8
ºC
Note : Un Handbook de chimie indique que sous deux atmosphères, l’eau bout à 121 ºC.
________________________________________
Problème Nº 12
Le volume molaire de l’eau est de 18 cm3 et la masse volumique de la glace est de 0,917 g · cm-3. En déduire au voisinage de 0 °C la valeur du rapport dP/dT correspondant à la courbe de fusion de la glace. On indique que la chaleur latente de fusion de la glace est de 80 calories par gramme à cette température.
CORRIGÉ
Le volume molaire de la glace est telle que :
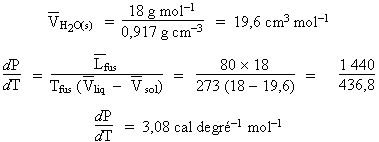
Dans le système international, il faut d’abord transformer la chaleur latente de fusion de la glace :
|
|
= 80 cal/g ´ 18 g/mol ´ 4,18 J/cal = 6 020 J/mol |
|
|
= - 13,78 J degré-1 mol-1 |
________________________________________
Problème Nº 13.
Règle de Pictet-Trouton
À partir des températures
et des enthalpies de vaporisation sous pression normale obtenues d’une source
appropriée, calculez la valeur de la constante a pour la série des alcanes
normaux (C1 à C10), pour la série des 2-cétones (de la propanone à la
2-heptanone) ainsi que pour la série des alcools linéaires ( C1 à C6). Que pensez-vous du comportement relatif des valeurs de a
des alcanes, des cétones et des alcools ?
CORRIGÉ
La règle de PICTET – TROUTON est donnée par la relation :
DHvap = a Te
Le problème se résout en obtenant les températures et les énergies d’ébullition des trois séries de composés. On les obtient à partir du site web suivant : http://webbook.nist.gov/chemistry/.
On remplit alors le tableau suivant en divisant l’enthalpie de vaporisation exprimée en J/mol par la température en Kelvin.
| Nb
d’atomes de carbone |
DH (kJ/mol) | Téb (K) | a
J/(mol K) |
Nb
d’atomes de carbone |
DH (kJ/mol) | Téb (K) | a
J/(mol K) |
| Alcanes linéaires | n-alcools | ||||||
| 1 | 8,17 | 111 | 73,60 | 1 | 35,21 | 337,8 | 104,23 |
| 2 | 14,70 | 184,6 | 79,63 | 2 | 38,56 | 351,5 | 109,70 |
| 3 | 18,80 | 231,1 | 81,35 | 3 | 41,44 | 370,3 | 111,91 |
| 4 | 22,40 | 273 |
82,05 | 4 | 43,29 | 390,6 | 110,83 |
| 5 | 25,80 | 309,2 | 83,44 | 5 | 44,36 | 411 | 107,93 |
| 6 | 28,85 | 341,9 | 84,38 | 6 | 44,50 | 430 | 103,49 |
| 7 | 31,77 | 371,5 | 85,52 | Moyenne = 108,0 ± 3,5 | |||
| 8 | 34,40 | 398,7 | 86,28 | 2-alcanones | |||
| 9 | 36,90 | 423,8 | 87,07 | 3 | 29,10 | 329,3 | 88,37 |
| 10 | 38,75 | 447,2 | 86,65 | 4 | 31,30 | 353 | 88,67 |
| Moyenne = 83,0 ± 4,1 | 5 | 33,44 | 375 | 89,17 | |||
| 6 | 36,35 | 400 | 90,88 | ||||
| 7 | 39,50 | 424 | 93,16 | ||||
| Moyenne = 90,0 ± 2,0 | |||||||
En ce qui concerne les séries des alcanes et des alcools, les valeurs obtenues pour a sont celles rapportées dans le cours. La valeur correspondante pour la série des 2-alcanones est telle que :
a =
90,0 ± 2,0 J/(mol K).
Un examen plus approfondi des résultats montre une situation un peu plus complexe. Dans la série des alcanes, la valeur de a tend à augmenter avec le nombre d’atomes de carbone. Le tracé du graphe
a = f(nombre d’atomes de carbone)
en utilisant une feuille Excel par exemple, est très explicite (Fig. 1). Au contraire dans la série des alcools, la valeur de a semble passer par un maximum correspondant au propanol (Fig. 2). Enfin, dans la série des 2-alcanones la valeur de a semble augmenter avec le nombre d’atomes de carbone (Fig. 3). Il existe donc des facteurs autres que le nombre d’atomes de carbone qui influencent la température d’ébullition. Le moment dipolaire évidemment présent dans la série des alcools est sans doute de ceux-ci. Le fait que la constante a croît en passant des alcanes, aux 2-cétones, puis aux alcools primaires est en accord avec cette assertion.
|
|
Figure 1. Règle de PICTET - TROUTON et les alcanes linéaires.
|
|
Figure 2. Règle de PICTET - TROUTON et les alcanes linéaires.
|
|
Figure 3. Règle de PICTET - TROUTON et les alcanes linéaires.
Néanmoins, la formule de PICTET-TROUTON donne une valeur approximativement convenable de la température d’ébullition.
________________________________________
Problème Nº 14. Formule
de Nekrassow
En
utilisant seulement les incréments relatifs apparaissant dans le tableau 4.5,
comparez les températures d’ébullition calculées et réelles (sous la
pression atmosphérique) du méthane, du propane, du 1,3-pentadiène et du benzène.
Qu’en tirez-vous comme conclusions ?
CORRIGÉ
________________________________________
Problème Nº 15. Tension de surface et Point critique
Déterminez la
température critique du benzène à partir des données suivantes ;
|
Température
|
Tension de surface |
Densité |
|
25 |
28,2 |
879 |
|
50 |
25,0 |
860 |
|
75 |
21,9 |
821 |
CORRIGÉ
La formule de RAMSAY – SHIELDS relie la tension de surface, la densité et la température critique (équation 4.4) :
|
|
=
k (Tc – T – 6) |
Pour
l’utiliser, on en prend le logarithme :
Ln
s
+ 2/3 (Ln M – Ln dliq) = Ln k + Ln T'
où T'
= Tc – T – 6
Cette
équation n’est pas directement utilisable puisqu’elle comprend un facteur
Ln k qu’on ne connaît pas. Pour
se débarrasser de ce facteur il suffit d’appliquer cette formule à deux températures
différentes et par différence le Ln k disparaîtra de lui-même.
À
la température T1,
on obtient :
Ln
s1
+ 2/3 (Ln M – Ln dliq1)
= Ln k + Ln T'1
où T'1
= Tc – T1
– 6
À
T2,
on a :
Ln
s2
+ 2/3 (Ln M – Ln dliq2)
= Ln k + Ln T'2
où T'2
= Tc – T2
– 6
Par
différence,
Ln
s1
– Ln s2
+ 2/3 (Ln dliq2
– Ln dliq1)
= Ln T'1
– Ln T'2
Ou
encore :
Ln
(s1/
s2)
+ 2/3 Ln (dliq2
/ dliq1)
= Ln (T'1
/ T'2)
Il
ne reste qu’à effectuer l’application numérique entre 25 et 50 °C, puis
entre 50 et 75 °C. Ainsi, entre 25
et 50 °C, l’application numérique produit :
Ln
(28,2/25,0) + 2/3 Ln (879/860)
= Ln (T'1
/ T'2)
0,120
45 +
2/3 ´
0,021 852 = Ln [(Tc – T1
– 6) / (Tc – T2
– 6)]
0,142
30 =
Ln [(Tc – T1
– 6) / (Tc – T2
– 6)]
1,152
92 =
(Tc – 31) / (Tc – 56)
Tc
= 219,5 °C
= 492,5 K
De
la même manière, entre 25 et 75 °C, l’application numérique produit :
Ln
(28,2/21,9) + 2/3 Ln (879/821)
= Ln (T'1
/ T'2)
0,252
83 +
2/3 ´
0,068 26 = Ln [(Tc – T1
– 6) / (Tc – T2
– 6)]
0,298
34 =
Ln [(Tc – 31) / (Tc – 81)]
1,347
62 =
(Tc – 31) / (Tc – 81)
Tc
= 224,8°C
= 497,8 K
La
littérature donne le résultat suivant :
Tc(benzène) =
562 K. L’accord n’est
donc pas si bon que cela. Même après avoir tenu compte du fait que la formule de
RAMSAY – SHIELDS attribue au liquide une tension de surface nulle 6 degrés en
dessous de la température, le résultat est encore loin de la valeur réelle.
Notons que le résultat indique un ordre de grandeur convenable.
Notes :
1-
Il serait illusoire de chercher, selon la même méthode, la valeur obtenue
entre les températures de 50 et de 75 °C.
Le résultat ne serait pas, en effet, indépendant des deux autres.
2- Il est indifférent d'introduire les températures en Kelvin ou en degrés Celsius dans la formule de RAMSAY - SHIELDS. En effet, comme la formule traite de la différence entre la température critique et une température quelconque, Tc et T, la différence d'échelle disparaît justement dans cette différence. De la même manière, la formule utilisée, logarithmique de rapport fait fi des unités utilisées puisque les facteurs correspondant au choix des unités disparaissent dans les rapports.
3- Finalement, on pourrait essayer d’appliquer à lune des trois températures le résultat numérique trouvé pour calculer la constante k de la formule de RAMSAY – SHIELDS.
________________________________________
N° 16. Diamètre moléculaire
Le coefficient de viscosité du chlore à la température de 20 °C et sous la pression atmosphérique est de 147,0 micropoises. Calculer le libre parcours moyen de la molécule en phase gazeuse ainsi que son diamètre moléculaire. Comparez votre résultat à celui obtenu à partir de la loi de Van der Waals qui indique que la valeur du covolume pour le chlore moléculaire est de 56,2 cm3/mole.
CORRIGÉ
L’application de la formule 4.7 permet de trouver le libre parcours moyen des molécules en phase gazeuse (en utilisant le système CGS) :
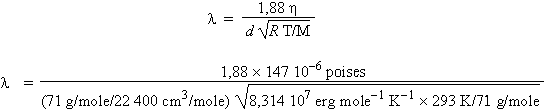
l
= 4,71 10-6
cm
Le Le diamètre moléculaire, d, peut être calculé à travers une relation déjà établie au chapitre 2, équation 2.30 :
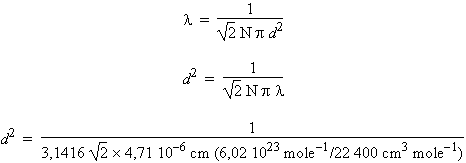
d2
= 17,7 10-16
cm2
d
= 4,21 10-8
cm
ou
encore :
d = 0,421 nm
Le covolume déterminé à travers la loi de Van der Waals correspond au volume physique des molécules en phase gazeuse. On dispose ainsi d’une méthode pour déterminer le volume et donc le diamètre de chacune des molécules. Par conséquent, en C.G.S., :
4/3 p r3 = covolume / N
1,33 ´
3,1416 r3
= 56,2 cm3/mole
/(6,02 1023 /mole)
r3
= 22,34 10-24
cm3
r
= (22,34)1/3 10-8
cm
r
= 2,82 10-8
cm
d =
0,562 nm
Il est intéressant de voir que les résultats, mêmes s’ils montrent un même ordre de grandeur, indiquent une différence de 0,14 nm, soit 25 % par rapport à la valeur déduite du covolume, soit 33,3 % par rapport à celle déduite de la mesure de la viscosité. Les deux approches expérimentales « voient » les molécules de chlore selon deux « lunettes » très différentes. Il est d’intérêt d’apprécier cette différence. Une mesure à l’aide des rayons X du cristal de chlore très probablement conduirait à une autre valeur du diamètre moléculaire.
___________________________________