Chapitre 3
Problème Nº 1
CORRIGÉ
________________________________________
Problème Nº 2 Loi de Van der Waals
La loi de VAN DER WAALS indique que le volume physique (le covolume) d’une mole d’éthane est de 0,0638 litre/mol. À partir de cette valeur, calculez :
a- le diamètre moyen des molécules et le libre parcours moyen (conditions TPN);
b- la vitesse moyenne et la vitesse quadratique moyenne des molécules (conditions TPN);
c- le nombre de collisions par seconde.
CORRIGÉ
a- En supposant que les molécules sont sphériques, si r est le rayon moyen d’une molécule, alors,
4/3 p r3 N = 0,0638 litre
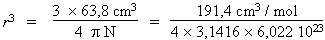
r3
= 25,3
10-24
cm3
r
= 2,92
10-8
cm =
0,292 nm
d
= 0,584 nm
Le
libre parcours moyen est donné par la relation :
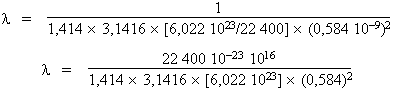
l
=
24,8 10-7
cm
l
= 2,48 10-6
cm = 2,48 10-8
m
b-
La vitesse moyenne des molécules est donnée par la relation (la
masse molaire de l’éthane est de 0,030 kg/mol dans le système SI) :
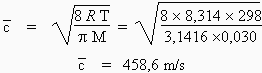
La
vitesse quadratique moyenne des molécules est donnée par la relation
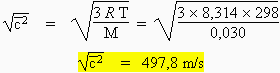
d-
Le nombre de collisions par seconde est donné par
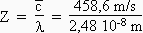
Z
= 1,85 1010
collisions par seconde
________________________________________
Problème Nº 3 Loi de Van der Waals
Les coefficients a et b de l’équation de VAN DER WAALS pour l’éthane, C2H6, sont respectivement 5,41 litre2 atm mol-2 et de 0,064 06 litre mol-1. Calculez le diamètre moyen des molécules d’éthane.
CORRIGÉ
Dans la formule de VAN DER WAALS, le coefficient b mesure le volume réel des molécules, le volume qu’occupent réellement une mole de molécules. On a donc :
|
Volume d’une molécule = |
|
Volume d’une molécule = 10,64 10-24 cm3
On peut ainsi calculer le rayon de la molécule à travers la relation :
(4/3)p r3 = 10,64 10-24cm3
r3 =
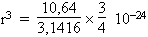 |
= 2,35 10-24 cm3 |
r = 1,34 10-8 cm
r = 1,34 10-10 m = 0,134 nm
________________________________________
Problème Nº 4
Un échantillon de
gaz carbonique contient n molécules
à une pression de 120 atm et une température de 70 ºC.
Calculez en fonction de n le
produit P V dans le système litre-atmosphère, en calories et dans le système
international
a- par la formule de BOYLE-MARIOTTE et
b- par la formule de BERTHELOT
CORRIGÉ
La loi de BOYLE-MARIOTTE est : P V = n R T dans laquelle, ici, T = 273 + 70 = 343 K.
Dans
le système litre-atmosphère et le système international (SI), on obtient :
P V = 1,987 ´
343 ´
n =
686 n calories ou encore
P V = 0,082 ´ 343 ´ n = 28,1 n litre-atmosphère, ou encore
P V = 8,314 ´ 343 ´ n = 2851,7 n joules
La loi de BERTHELOT utilise les données critiques de la molécule. Pour le gaz carbonique, la littérature (un Handbook…) donne les valeurs suivantes : PC = 73,1 atm et TC = 304 K. D’où,
![]()
Il faut
remarquer que l’expression entre crochets n’a pas d’unité : c’est
un nombre sans dimension. On peut
donc calculer son expression en utilisant un système d’unité quelconque
pourvu qu’il soit homogène. En
remplaçant les valeurs littérales par leur valeur numérique, on obtient :
![]()
P
V =
n R T [ 1 + 0,1023 ( 1
- 6 ´
0,7855) ]
P
V =
n R T (1
+ 0,1023 ( - 3,713 )
P
V =
n R T (0,6201)
En SI, on obtient donc :
P
V = 8,314 ´
343 ´
n ´
0,6201
P
V =
1768,5 n joules
Etc.,
etc.
________________________________________
Problème Nº 5
La densité de l’éthanol gazeux est donnée en fonction de la température. Déterminez graphiquement la température critique de l’éthanol. Essayez d’en déduire la densité critique de ce composé.
| T (°C) | 100 | 150 | 200 | 220 | 240 |
| rliq | 0,716 | 0,649 | 0,557 | 0,496 | 0,382 |
| rvap | 0,0035 | 0,019 | 0,051 | 0,085 | 0,172 |
CORRIGÉ
Pour répondre aux questions posées, il faut se souvenir qu’au point critique, les propriétés physiques du liquide et de la vapeur d’un composé se rejoignent. Il faut donc porter sur un graphe la propriété, dans le cas présent la densité, mesurée dans les deux phases en fonction de la température (Fig. 1)*. L’examen attentif du graphe permet de voir deux courbes qui convergent vers une température que l’on peut estimer visuellement :
TC = 246 ± 1 °C.
|
|
Figure 1. Variations de la densité de l'éthanol liquide et gazeux en fonction de la température.
* NOTE : Le tracé de ces courbes sur un papier millimétré est évidemment de bien meilleure précision et est fortement conseillé.
La détermination de la densité du fluide à la température critique est un peu moins évidente : elle ne peut être plus précise que la détermination du sommet de la courbe qui apparaît sur le graphe. On peut cependant l’estimer à 0,26 ± 0,02.
Il existe une méthode relativement simple pour affiner cette lecture. En première approximation, le lieu géométrique des milieux des segments (AA’, BB’, … sur le graphe) qui joignent les densités des deux phases à une température donnée est une droite. Cette droite MN passe nécessairement par le sommet de la courbe apparaissant sur le graphe. L’interception de cette droite avec la courbe indique la densité critique suivante :
rC = 0,27 ± 0,01.
Les valeurs obtenues dans sont :
TC = 246 ± 1 °C et rC = 0,27 ± 0,01.
________________________________________
Problème Nº 6
Sachant que la pression critique et la température critique du butane normal sont respectivement 37,5 atm et 152 °C, calculez les constantes de VAN DER WAALS de ce gaz.
CORRIGÉ
Les constantes critiques d’un gaz sont reliées aux coefficients de l’équation a et b de VAN DER WAALS à travers les relations suivantes :
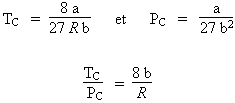
Dans
le système d’unités « litre – atmosphère »
on obtient :
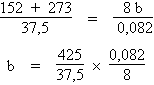
b
= 0,123 litre / mol
Par
ailleurs, a
= 27 b2
PC =
27 ´
0,1232 ´
37,5 =
15,31 litre2 atm
mol-2
a
= 15,31
litre2 atm mol-2
________________________________________
Problème Nº 7 Diamètre de molécules
On donne les constantes critiques du monoxyde de carbone, CO :
Tc = 134,4 K, Pc = 35,1 atm et Vc = 90,0 cm3 mol-1
a- Calculez les constantes de l’équation de VAN DER WAALS dans le système litre-atmosphère et dans le système SI.
b- En déduire le diamètre moyen des molécules d’oxyde de carbone.
CORRIGÉ
a- Les équations 3.3a et 3.3b permettent de relier les constantes de VAN DER WAALS aux conditions de volume molaire et de pression critiques, Vc et Pc :
Vc
= 3 b
et a =
27 Pc b2
Vc
= 0,090 litre/mol = 3 b
D’où :
b
= 0,030 litre/mol
a
= 27 × 35,1 × (0,030)2
a
= 0,852 93 unités du système
d'unités litre – atmosphère.
b- Le volume réel des molécules de monoxyde de carbone est donc de 0,090 litre/mol ou encore de 90 10-6 m3/mol. Le volume d’une seule molécule est donc :
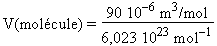 |
= 14,942 10-29 m3 = 0,149 42 10-27 m3 |
En
assimilant la molécule à une sphère de volume égale à 4/3 p
r3, on peut en calculer le rayon r :
4/3
p
r3 =
0,149 42 10-27 m3
et
r3 = 0,149 42 10-27 m3
/
4/3 p
= 0,0356 73 10-27 m3
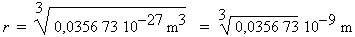
r
=
0,1528 nm
________________________________________
Problème Nº 8 Densité
a- Les coefficients de l’équation de KAMERLINGH ONNES pour le monoxyde de carbone sont à 0 °C (la pression P est exprimée en atmosphère et les volumes le sont en litre mol-1) :
A = 22,414 ; B = - 1,4825 10-2 ; C = 9,823 10-5 ; D = 7,721 10-8 et E = 1,947 10-11
Calculez la densité de CO à 0 °C et sous une pression de 100 atm.
b- Calculez la même densité en utilisant la loi de MARIOTTE dans les mêmes conditions expérimentales.
c- Faire le même calcul en utilisant l’équation de VAN DER WAALS. Les valeurs des coefficients de cette équation ont été calculées dans le problème précédent.
CORRIGÉ
a- L’équation de KAMERLINGH ONNES est donnée par la relation 3.11 :
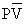 |
= A + B P + C P2 + D P3 + … |
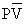 |
= 22,414 - 1,4825 10-2 P + 9,823 10-5 P2 + 7,721 10-8 P3 + 1,947 10-11 P4 |
En remplaçant P par sa valeur, 100 atm, on calcule le volume molaire dans les conditions proposées :
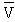 |
= 22,414/P - 1,4825 10-2 + 9,823 10-5 P + 7,721 10-8 P2 + 1,947 10-11 P3 |
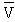 |
= 0,224 14 - 0,0148 25 + 9,823 10-3 + 7,721 10-4 + 1,947 10-5 |
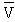 |
= 0,224 14 - 0,0148 25 + 0,009 823 + 0,000 7721 + 0,000 019 47 |
|
|
= 0,21 993 litre/mol |
On
voit que le dernier terme ajoute seulement 2 unités sur la 5e décimale.
La densité d est le rapport de la masse molaire sur le volume
occupé. À 0
°C
et sous la pression de 100 atmosphères, la densité est donc :
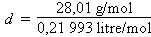
d =
127,36 g/litre
b. Le même calcul se fait aisément avec l’équation de BOYLE-MARIOTTE :
|
|
= RT et RT/P = |
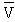 |
R
est la constante des gaz parfaits. Elle
a la valeur 8,1441 J/(mol K), donc dans le SI.
Dans le système litre – atmosphère, elle prend la valeur 0,082 054
litre–atm mol-1
K-1.
Si on ne se souvient pas de la valeur de la constante des gaz parfaits il
suffit d’appliquer la loi de BOYLE-MARIOTTE de la manière suivante :
P
V = RT et
R =
P
/ T
i-
en SI :
R
= 101 325 N/m
× 0,022 413 m3
mol-1
/ 273,15 K = 8,3143 J/(mol K)
ii-
en
litre-atmosphère :
R
= 1 atm
× 22,413 litre mol-1
/ 273,15 K = 0,082 054
litre-atm/K
En revenant à la loi de BOYLE-MARIOTTE, on obtient :
|
|
= RT/P = 0,082 054 × 273,15 /100 |
|
|
= 0,224 13 litre/mol |
et la densité devient :
d = 124,97 g/litre
L’écart avec la valeur trouvée en utilisant l’équation de KAMERLINGH ONNES est peu important, au moins pour ce gaz et dans les conditions prescrites : 0 ºC et 100 atmosphères.
c- Le calcul est moins évident avec la formule de VAN DER WAALS :
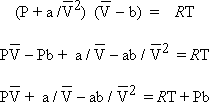
On peut multiplier chacun des membres de cette équation par le carré du volume molaire, à l’évidence, ce terme est différent de zéro :
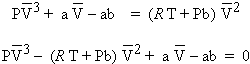
On
obtient ainsi une équation du troisième degré par rapport au volume molaire
recherché. Cette équation a
trois racines. Le problème physique demande que le résultat numérique ne
soit un nombre imaginaire et de plus qu’il soit positif. En remplaçant les valeurs littérales par leurs valeurs numériques,
on obtient :
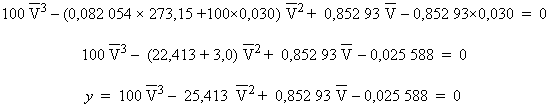
Cette
équation du 3ème degré en V n’est pas aisée à solutionner.
On dispose cependant d’un outil intéressant, le logiciel Excel, qui
permet de trouver au moins une solution acceptable en utilisant une approche itérative.
Comme la réponse recherchée doit se trouver aux environs de 0,20 –
0,24 litre/mol, on essaie successivement différentes valeurs numériques du
volume molaire. Un premier essai
est fait entre 0,15 et 0,25 litre/mol :
| V | 100 V3 | 25,413 V2 | 0,852 93 V | y |
| 0,15 | 0,338 | 0,572 | 0,128 | -0,0808 |
| 0,16 | 0,410 | 0,651 | 0,136 | -0,0789 |
| 0,17 | 0,491 | 0,734 | 0,145 | -0,0726 |
| 0,18 | 0,583 | 0,823 | 0,154 | -0,0611 |
| 0,19 | 0,686 | 0,917 | 0,162 | -0,0439 |
| 0,20 | 0,800 | 1,017 | 0,171 | -0,0204 |
| 0,21 | 0,926 | 1,121 | 0,179 | 0,0101 |
| 0,22 | 1,065 | 1,230 | 0,188 | 0,0480 |
| 0,23 | 1,217 | 1,344 | 0,196 | 0,0941 |
| 0,24 | 1,382 | 1,464 | 0,205 | 0,1489 |
| 0,25 | 1,563 | 1,588 | 0,213 | 0,2130 |
La solution pour y = 0 se trouve entre 0,20 et 0,21. On reprend le même type d’itérations entre 0,200 et 0,210. Le résultat montre que la solution se trouve entre 0,206 et 0,207. Finalement, un autre essai entre 0,2060 et 0,2070 montrerait que le résultat se trouve entre 0,2069 et 2070. Finalement, un dernier essai (tableau suivant) montre que la solution est proche de 0,20695.
| V | 100 V3 | 25,413 V2 | 0,852 93 V | y |
| 0,2069 | 0,886 | 1,088 | 0,176 | -0,000 151 |
| 0,206 91 | 0,886 | 1,088 | 0,176 | -0,000 119 |
| 0,206 92 | 0,886 | 1,088 | 0,176 | -0,000 088 |
| 0,206 93 | 0,886 | 1,088 | 0,176 | -0,000 056 |
| 0,206 94 | 0,886 | 1,088 | 0,176 | -0,000 024 |
| 0,206 95 | 0,886 | 1,088 | 0,177 | 0,000 008 |
| 0,206 96 | 0,886 | 1,088 | 0,177 | 0,000 040 |
| 0,206 97 | 0,887 | 1,089 | 0,177 | 0,000 072 |
| 0,206 98 | 0,887 | 1,089 | 0,177 | 0,000 103 |
| 0,206 99 | 0,887 | 1,089 | 0,177 | 0,000 135 |
| 0,2070 | 0,887 | 1,089 | 0,177 | 0,000 167 |
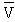 |
= 0,206 95 litre |
ou encore ou V = 0,206 95 litre/mole
La densité devient :
d = 135,35 g/litre.
___________________________________