|
|
|
C’est maintenant le temps d’étudier les comportements et surtout les propriétés de l’état solide. Bien sûr certaines propriétés observées et rapportées dans les deux chapitres qui précèdent s’appliquent aussi à l’état solide. Citons de manière non exhaustive, l’absorptiométrie, la viscosimétrie, … On ne retiendra pour étude dans ce présent chapitre que les propriétés propres à l’état solide. Quelles sont-elles ?
|
Chaque composé chimique est constitué d’un groupe d’atomes. À l’état solide, chaque molécule s’associent à ses voisines pour créer un empilement géométrique de telle façon que toute autre structure ou empilement demanderait une surcroît d’énergie pour obtenir l’édifice solide (à l’équilibre). En d’autres termes, l’édifice solide atteint est celui de moindre énergie.
Pour combiner des structures moléculaires dans un empilement, il n’y a pas de nombreuses manières. En se basant seulement sur des considérations de géométrie et surtout de symétrie, seules 230 formes cristallines peuvent être obtenues. La grande majorité de ces structures ont été observées.
Ces 230 structures cristallines, par affinité de symétrie, peuvent être réarrangées en 32 classes et ces classes se résument en 7 systèmes cristallins (Tableau 6.1). Chaque système est défini par 3 axes et les trois angles entre ces trois axes. La présence (ou l’absence) d’éléments de symétrie déterminent chacun de ces systèmes (Fig. 6.1).
Tableau 6.1. Les 7 systèmes cristallins
|
Système |
Caractéristiques |
Symétrie maximum |
|
|
Axes |
Angles |
||
|
Triclinique |
a
¹
b
¹
c |
a
¹
b
¹
g |
0 |
|
Monoclinique |
a
¹
b
¹
c |
a
=
b = 90
¹
g |
1 plan, 1 axe |
|
Orthorhombique |
a
¹
b
¹ c |
a
=
b =
g = 90 |
3 plans, 3 axes |
|
Quadratique |
a = b
¹
c |
a
=
b =
g = 90 |
5 plans, 5 axes |
|
Hexagonal |
a = b
¹
c |
a
=
b = 90;
g = 120 |
7 plans, 7 axes |
|
Rhomboédrique |
a = b = c |
a
=
b =
g
¹
90 |
7 plans, 7 axes |
|
Cubique |
a = b = c |
a
=
b =
g = 90 |
9 plans, 13 axes |
|
|
Figure 6.1. Systèmes d’axes quelconques.
2.
Les propriétés des cristaux
2.1. La structure cristalline
Il existe donc sur le plan de la symétrie 230 structures cristallines, 32 classes et 6 (ou 7 selon que l’on intègre ou nom le système rhomboédrique dans le système hexagonal) systèmes cristallins. Il est cependant intéressant d’avoir une classification qui tienne compte de la structure interne des cristaux. Un cristal est constitué par la répétition dans toutes les directions d’une unité structurale fondamentale appelé groupe d’espace.
À son tour, chaque groupe d’espace est constitué d’un empilement particulier d’atomes, d’ions, de molécules arrangé pour donner une configuration géométrique particulière. Ce sont les réseaux de BRAVAIS (Tableau 6.2).
Tableau 6.2. Les 14 réseaux de BRAVAIS et les groupes d’espace
|
Systèmes |
Réseaux |
Nombre de groupes
d’espace |
Exemples |
|
Triclinique |
simple |
2 |
H3BO3,
K2Cr2O7 |
|
Monoclinique |
simple |
13 |
AgS, As4 |
|
Orthorhombique |
simple |
59 |
TiO2, Ag3Sb,
PtS |
|
Quadratique |
simple |
68 |
Ni4As8 |
|
Hexagonal |
simple |
52 * |
Zn, Cd, Ti, CaCO3 |
|
Rhomboédrique |
simple |
CaCO3
(calcite), Bi |
|
|
Cubique |
simple |
36 |
Po |
|
Total : 7 |
Total : 14 |
Total : 230 |
|
* Nota : le rhomboèdre est parfois classé dans le système hexagonal.
Les structures simples se retrouvent dans chacun des 7 systèmes : on y trouve un atome (ou un groupe d’atomes aux 8 sommets du parallélépipède (Fig. 6.2). Comme chaque atome ou groupe d’atomes est partagé dans 8 parallélépipèdes (motifs), on a donc 1 atome ou groupe d’atomes par motif.
|
|
Figure 6.2. Les réseaux simples.
Les trois structures orthorhombique, quadratique et cubique adoptent le réseau centré, c’est-à-dire qu’au centre du motif on retrouve un atome ou un groupe d’atomes. On a maintenant 2 atomes ou groupes d’atomes par motif (Fig. 6.3).
|
|
Figure 6.3. Les réseaux centrés.
Les systèmes orthorhombique et monoclinique admettent la structure à deux faces centrées : on trouve un atome ou un groupe d’atomes au centre de deux faces opposées. Ces deux atomes ou groupes d’atomes sont partagés entre deux parallélépipèdes, on trouve donc 2 atomes ou groupes d’atomes par motif (Fig. 6.4).
|
|
Figure 6.4. Les réseaux à deux faces centrées.
Finalement, les systèmes orthorhombiques et cubiques admettent la structure à toutes faces centrées. Chaque motif contient 4 atomes ou groupes d’atomes (Fig. 6.5).
|
|
Figure 6.5. Les réseaux à toutes faces centrées.
2.2.
Les composés uniaxes et bi-axiaux
Lorsqu’un agrégat macroscopique forme une structure équivalente dans toutes les directions, la structure correspondante doit avoir des propriétés semblables dans toutes ces directions. On dit alors que ces substances sont isotropes. Un observateur immergé au sein de cette structure apercevrait le même paysage quelle que soit la direction de son regard. Par exemple, un gaz, un liquide homogène, un solide amorphe,…
Pour les substances cristallines, seules celles qui cristallisent dans le système cubique ont cette équivalence dans les trois directions. L’indice de réfraction, le coefficient de dilatation thermique linéaire, les conductibilités électrique et thermique,… sont les mêmes. On dit aussi qu’elles sont isotropes. Pour les autres cristaux, ils présentent tous des propriétés d’anisotropie : ils sont anisotropes.
Par exemple, le coefficient de dilatation thermique de l’iodure d’argent AgI est positif dans une direction et négatif dans une autre. En ce qui concerne les propriétés optiques, les cristaux sont subdivisés en cristaux uniaxes et en cristaux bi-axiaux. Ce tableau donne un aperçu assez large de divers propriétés. Les tableaux 6.3 et 6.4 donnent des exemples de comportement de diverses propriétés physiques de cristaux uniaxes selon l’axe d’observation dont l’indice de réfraction, propriété déjà abordée au chapitre 5.1.1.
Tableau 6.3. Indices de réfraction et constantes diélectriques de cristaux uniaxes
|
Composés |
Structure |
nD |
Constante
diélectrique |
|
Rutile, TiO2 |
quadratique |
2,616 |
86 (108)
a |
|
Cassitérite, SnO2 |
quadratique |
2,006 |
23,4 (1012) |
|
Béryl, |
hexagonal |
1,577 |
7,02 (104) |
|
Quartz, SiO2 |
rhomboédrique |
1,543 |
4,34 (3 107) |
| Sapphire, Al2O3 | hexagonal |
1,766 1,758 |
8,6 (3 108) 10,55 (3 108) |
| Lithium niobate, LiNbO3 | hexagonal |
2,237 2,158 |
|
|
Smithsonite,
ZnCO3 |
rhomboédrique |
1,848 |
9,3 (1012) |
|
Calcite, CaCO3 |
rhomboédrique |
1,656 |
8,5 (104) |
|
Apatite, Ca5(PO4)3(OH,F,Cl) |
hexagonal |
1,648 |
9,50 (3 108) |
|
a :
la 1e valeur est donnée perpendiculairement et la 2e
parallèlement à l’axe optique. |
|||
Tableau 6.4. Conductivité thermique et coefficient de dilatation thermique de quelques composés uniaxes
Composés
|
Conductivité
thermique |
Coefficient
de dilatation thermique |
|
Rutile, TiO2 |
8,8 a |
7,14 a |
|
Quartz, SiO2 |
6,5 |
13,37 |
| Sapphire, Al2O3 |
33 35,1 |
5,6 5 |
|
Cassitérite, SnO2 |
55 98 |
4,0 3,7 |
|
Calcite, CaCO3 |
|
-
4 |
|
Lithium niobate LiNbO3 |
4,19 4,6 |
4,1 14.8 |
|
Zincite, ZnO |
60 |
4,75 |
|
a : la 1ère valeur est
prise perpendiculairement et la 2e parallèle au plan
[001]. |
||
Les cristaux uniaxes sont ceux des systèmes quadratiques et hexagonaux. Ils possèdent deux valeurs de leurs indices de réfraction. Les cristaux biaxiaux sont ceux des systèmes orthorhombiques, monocliniques et tricliniques. Ils ont 3 indices de réfraction (Tableau 6.4).
Tableau 6.5. Indices de réfraction de quelques composés biaxiaux
|
Composés biaxiaux |
Structure |
Indice de réfraction |
|
HgO |
orthorhombique |
2,37 – 2,5 – 2,65 |
|
Mn(TaO3)2 |
orthorhombique |
2,22 – 2,25 – 2,29 |
|
MnSO4,H20 |
monoclinique |
1,562 – 1,595 –
1,632 |
|
FeSO4,H2O |
triclinique |
1,526 – 1,536 –
1,542 |
|
PbSO4,PbO |
triclinique |
1,93 – 1,99 – 2,202 |
|
Li2CO3 |
monoclinique |
1,426 – 1,567 –
1,572 |
2.3. Une mesure rapide de l’indice de réfraction
des solides
Une méthode rapide consiste à immerger dans un liquide d’indice de réfraction connu le solide dont on veut connaître de manière suffisamment précise son propre indice de réfraction. En effet, un solide plongé dans un liquide transparent demeure visible tant et aussi longtemps que les indices de réfraction du liquide et du solide sont différents. Le solide est entouré d’une ligne sombre et nette, elle même entourée d’une zone lumineuse plus ou moins large. Dès l’instant où le liquide et le solide auront le même indice de réfraction, le solide aura tendance à disparaître puisque les rayons lumineux continueront leur cheminement en ligne droite.
Cette méthodologie exige entre autres conditions :
- que le solide est insoluble dans le liquide ;
- qu’il n’existe aucune interaction chimique entre le solide et le liquide.
Cette méthode implique que l’on ne saura pas distinguer les différents indices des composés uni ou biaxiaux, sauf si on dispose de gros cristaux que l’on saura orienter convenablement pour l’observation. Cette méthode requière également que l’on dispose d’une série de liquides couvrant l’ensemble des indices de réfraction possible (Tableau 6.6).
Tableau 6.6. Exemples de liquides utilisables pour la méthode par immersion
|
Liquide |
Formule |
nD |
Liquide |
Formule |
nD |
|
1,3-dichloropropane |
C3H6Cl2 |
1,446 |
2-nitrotoluène |
C7H7NO2 |
1,544 |
|
1,4-cinéole |
C10H16 |
1,456 |
2,4-xylidine |
C8H11N |
1,557 |
|
hexahydrophénol |
|
1,466 |
2-toluidine |
C7H9N |
1,570 |
|
décahydronaphthalène |
C10H8 |
1,477 |
aniline |
C6H5NH2 |
1,584 |
|
phthalate d’isoamyle |
|
1.486 |
bromoforme |
CHBr3 |
1,595 |
|
tétrachloroéthane |
C2H2Cl4 |
1,492 |
quinoline |
C9H7N |
1,622 |
|
pentachloroéthane |
C2HCl5 |
1,501 |
a-chloronaphthalène |
C10H7Cl |
1,633 |
|
1,3-dibromopropane |
C3H6Br2 |
1,513 |
diiodométhane |
CH2I2 |
1,738 |
|
chlorobenzène |
C6H5Cl |
1,528 |
|
|
|
2.4. Indice de réfraction et densité des solides
On a déjà vu au chapitre 5, Fig. 5.21, qu’un faisceau de lumière peut être assimilé à un ensemble de deux vecteurs champ électrique et champ magnétique perpendiculaires l’un à l’autre et perpendiculaires à la direction de propagation du faisceau. Au cours du trajet dans un matériel, le vecteur champ électrique interfère avec les champs électriques des électrons du milieu. Cette interaction est donc d’autant plus importante que la polarisabilité du milieu est grande. Cette interaction avec un cristal formé de liaisons covalentes sera différente, moins importante, que celle avec un cristal formé de liaisons ioniques, les électrons périphériques des ions y étant beaucoup moins fortement retenus par les noyaux. Il n’existe donc pas a priori de relation directe entre l’indice de réfraction et la densité des matériaux solides.
Un cas cependant bien documenté concerne une série de silices de différentes structures, SiO2. Tous les solides concernés, sont polymorphes : tridymite, cristobalite, … Ils diffèrent seulement par leur structure cristalline, les molécules de silice demeurant inaltérées. L’indice de réfraction varie de manière linéaire et croissante avec la densité, entre 1,44 à 1,84 tandis que la densité varie de 2,02 à 4,29.2.4.a. Indice de réfraction et pierres précieuses
Une propriété importante en joaillerie et plus particulièrement pour les pierres précieuses est l’indice de réfraction. À ce titre, le diamant présente un cas presque limite puisque son indice de réfraction est parmi ceux des plus élevés : nD = 2,4173. Combiné à une taille appropriée, la décomposition du spectre de lumière naturelle en ses composantes prend un effet maximum et donne à cette pierre précieuse son maximum de brillance et de feu.
|
|
Figure 6.6. Diamant taillé « royal ».
2.5. L’empilement de sphères
Un cas simple de structure se déduit de l’empilement de sphères. On a sans doute tous observé des billes, des balles de ping-pong, des balles de tennis. Leur forme sphérique leur permet de s’arranger de manière très géométrique dans un plan : chaque sphère est entourée ou est tangente à six autres sphères. Si on ajoute un deuxième plan de sphères, un deuxième étage, sur le premier, ce deuxième plan aura la même configuration et viendra se poser sur les parties creuses de cette surface. Il en sera ainsi des autres plans supérieurs successifs.
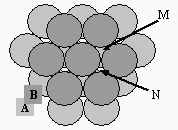 |
Figure 6.7. Empilement de sphères.
On remarque cependant qu’il existe au moins deux façons d’empiler le troisième plan (Fig. 6.7). Il peut tout d’abord se situer exactement sur le premier plan de telle sorte que si on considère une sphère de ce plan elle va se loger sur la position M de la figure 6.8A. Le résultat donne un empilement montré à la figure 6.8A. On a volontairement diminué la taille des sphères du 3e plan pour bien montrer la succession A B A B A B … Ce type d’empilement correspond à la structure hexagonale compacte.
|
|
Figure 6.8. Empilement de sphères par de plans de succession A B A B A B … ou A B C A B C ...
Il existe une seconde façon de poser le 3e plan qui permet une sphère de ce plan de ne pas se trouver à la verticale du 1er plan. Cette sphère ne peut bien évidemment se trouver à la verticale d’une sphère du 2nd plan : elle va se loger dans un creux engendré par ce second plan, en N sur la figure 6.7. La figure 6.8B montre le résultat de ce type d’empilement A B C A B C … Ce type d’empilement correspond à la structure cubique à faces centrées.
La figure 6.9 montre un système à faces centrées. Avec un peu d’imagination, on peut voir l’empilement des plans A B C A B C … représentés sur cette figure par les triangles bleu-vert.
|
|
Figure 6.9. Empilement de sphères dans un cube à faces centrées.
L’importance relative du vide dans les empilements.
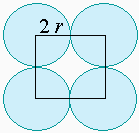
Imaginons un empilement de type cubique simple. Les atome s’arrangent dans un plan selon les sommets d’un carré. Le 2e plan, lui aussi construit sur le même carré vient se superposer exactement à la vertical du 1er carré (Fig. 6.10a). Si l’atome a un diamètre 2a, son volume V(atome) est égale à :
V(atome)
= 4/3 p
a3.
Le volume spatial qu’il occupe est égal à 8 a3. La fraction f de l’espace réellement occupée par l’atome est au rapport de ces deux valeurs, soit :
![]()
L’importance
du vide est donc le complément : 0,4764 ou 47,64 %.
 |
 |
 |
|
a |
b |
c |
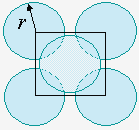
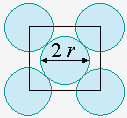
Figure
6.10.
Empilement de sphères dans des réseaux cubiques simples (a),
cubiques centrés (b) et à toutes faces centrées (c).
Note
: la figure montre dans chaque cas ce qu'on voit sur une face.
Le même calcul peut être repris dans le cas de l’empilement cubique centré. Dans ce cas, l’atome situé au centre du cube est tangent à chacun des huit atomes situés aux sommets du cube (Fig. 6.10b). Il est également situé au centre de la diagonale du cube. La longueur de cette diagonale est donc égale à deux fois le diamètre de l’atome : 4r. Selon le théorème de PYTHAGORE en trois dimensions, le carré de la longueur de cette diagonale est égal à trois fois le carré du côté du cube. Soit d la longueur de ce côté :
(4r)2 = 3 d2
et
![]()
Comme il y a deux atomes par cube – un au centre et 1/8 de chacun des huit atomes situés aux sommets du cube – la fraction de l’espace réellement occupé par ces deux atomes est telle que :
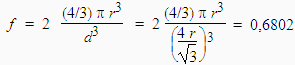
La fraction de l’espace occupée par l’atome est donc de 68,02 % et celle du vide, son complément : 31,98 %.
Dans le cas des structures cubiques à faces centrées (Fig. 6.10c), il y a 4 atomes dans chaque cube (Fig. 6.8). Par ailleurs, la diagonale d'un côté du cube a une longueur égale à 4a. La longueur du coté du cube, d, est telle que :
2 d2 = (4a)2
![]()
La fraction du volume occupé est donc :
![]()
Par conséquent, 74,04 % de l’espace est occupé et 25,96 % inoccupé. On obtient le même rapport dans le cas de l’empilement hexagonal compact.
Ainsi, de l’empilement cubique simple à l’empilement le plus compacte l’occupation de l’espace passe de 52 % à 74 %. Cette optimisation de l’occupation de l’espace est mise à profit par les solides monoatomiques et plusieurs structures ioniques. Bien évidemment, tous les atomes ne sont pas rigoureusement sphériques. Par ailleurs dans un solide diatomique, les deux atomes ne sont plus de la même grosseur. C’est ce que l’on retrouve également dans les solides ioniques comme NaI : l’ion iodure est un peu plus de 2 fois plus grand que l’ion Na+. Par ailleurs, les molécules plus compliquées peuvent avoir une structure très éloignée de la sphère parfaite. Dans ces cas, les structures cristallines les plus avantageuses ou préférées s’éloignent des systèmes très symétriques.
2.6. Le cas des structures cristallines ioniques
On vient de le voir, l’état cristallin possède un très haut niveau d’arrangement périodique dans l’espace : le motif se répète systématiquement sur un axe. Les structures cristallines ne constituent pas à proprement parler un cas à part. Ici les ions sont traités de la même manière que des atomes. Ainsi la structure cristalline ne constitue pas un empilement particulier d’atomes de sodium et d’atomes de chlore, mais bien plutôt un empilement d’ions Na+ et d’ions Cl-. Cet empilement est ici un empilement de type cubique à faces centrées (Fig. 6.11). De la même manière la structure cristalline du chlorure de césium correspond à la structure cubique centrée (Fig. 6.11).
|
|
Figure 6.11. Structure cristalline des chlorures de césium et de sodium.
Ces arrangements laissent supposer, et cela est le cas, que les entités NaCl n’existent pas en phase cristalline. La structure ressemble plutôt à un édifice tridimensionnel dans lequel le cation Na+ de 6 ions Cl-… alors qu’en phase gazeuse, la molécule NaCl est observable.
2.7. Le cas des structures covalentes
Les éléments constitutifs sont des atomes. Un cas bien connu est celui du carbone sous la forme diamant dont les atomes s’empilent de manière à former le tétraèdre régulier (Fig. 6.12). Il se forme un réseau tridimensionnel d’atomes de carbone, chaque atome étant lié par liaison covalente simple avec quatre autres de carbone. À la limite, le diamant ressemble structurellement à une macromolécule géante tridimensionnelle. Cette structure doit être comparée à la structure du carbone graphite. Dans ce dernier cas, le carbone prend une structure du benzène et forme une macromolécule géante en deux dimensions. Ces plans de nature aromatique sont espacés de 0,35 nm alors que les atomes de carbone, dans les feuillets, ne sont espacés que de 0,142 nm, dimension presque égale à la longueur de la liaison C-C dans le benzène : 0,139 nm. Cette différence de compaction se traduit par une différence dans la densité : d(graphite) = 2,25 kg/dm3 comparativement à d(diamant) = 3,51 kg/dm3.
|
|
Figure
6.12. Structure cristalline du
carbone graphite (à gauche) et
du carbone diamant (à droite).
Note : les deux figures ne sont pas à la même échelle : celle du
graphite étant plus petite.
Ce n’est cependant pas le cas général. On retrouve de nombreux cas (la très grande majorité) où les molécules conservent leur identité. C’est le cas de l’iode I2 (Fig. 6.13).
|
|
Figure 6.13. Structure de
l'iode dans son réseau cristallin.
Source :
http://www.rsc.org/pdf/molecularworld/third_dimension_intro.pdf
Cette page ne semble plus être accessible (2014-12-24).
2.8. Le polymorphisme
Une substance peut cristalliser dans un ou plusieurs systèmes cristallins dépendant de la température et de la pression. Ainsi, sur certaines régions du diagramme pression – température, la structure exigeant le moins d’énergie peut varier. Il existe donc des températures de transition d’une forme à l’autre : une forme est stable en-dessous et une autre forme est stable au-dessus de cette température de telle sorte qu’en augmentant la température on observe une transformation allotropique à une température de transition. À ce changement de phase est associée une chaleur latente de changement de phase, tout comme dans le cas de la fusion, de la sublimation, …
On appelle isomorphisme la propriété qu’ont deux ou plusieurs constituants chimiques de cristalliser dans la même structure. Par exemple, les sulfates de potassium K2SO4, de rubidium Rb2SO4, de césium C2SO4 ainsi que le séléniate de potassium K2SeO4,… cristallisent dans la même structure. Cette propriété est importante car elle permet bien souvent une solubilité plus ou moins importante d’un sel dans l’autre. Cette solubilité se fait remplacement des ions positifs entre eux et des ions négatifs entre eux.
Un composé peut présenter la propriété de polymorphisme : il peut exister et prendre différentes formes cristallines à l’état solide. Cependant, sauf à l’état d’équilibre entre deux structures, pour un couple de pression – température déterminé il ne peut exister que sous une seule forme cristalline : celle qui correspond à un minimum d’énergie. Le tableau 6.7 montre quelques exemples de changement de phases cristallines.
Tableau 6.7. Température de transition pour quelques structures cristallines
|
Substance |
Formes
cristallines |
|
Neptunium |
orthorhombique |
|
Fer |
cubique centré :
T < 910
°C |
|
Nitrate
d’ammonium |
quadratique
®
a-rhombique :
-17
°C |
|
Iodure d’argent |
hexagonal
®
cubique : 146,5
°C |
|
Nitrate d’argent |
rhombique
®
rhomboédrique : 159,6
°C |
|
Nitrate de
thallium |
rhombique
®
rhomboédrique : 75
°C |
|
Note : Mesures effectuées à la pression
atmosphérique. La flèche indique la transition physique. |
|
Bien sûr, pour une même substance, les propriétés d’une structure cristalline est différente de l’autre. Par exemple, la densité du neptunium passe de 20,45 à 19,36 (à 313 °C) et à 18,0 au dessus de 500 °C, donc en passant successivement des structures orthorhombique à quadratique puis à cubique.
On note aussi que le fer cristallise dans la même structure en dessous de 910 et au dessus de 1400 °C. Entre ces deux températures il acquiert la structure cubique à faces centrées.
3. Les défauts dans les arrangements cristallins
L’empilement régulier dans les trois directions du trièdre trirectangle des atomes, des ions, des molécules,… dans les cristaux est loin d’être toujours parfait. Dépendamment de la nature du défaut, ceux-ci peuvent être classés en plusieurs catégories. On retiendra ici les défauts de point et les défauts de ligne.
3.1. Les défauts de point
Les défauts de point sont caractérisés par la présence ou l’absence de motifs (atome, molécule, ion,… en un point particulier du cristal. La figure 6.14 montre les principaux cas d’espèce.
|
|
Figure 6.14. Défauts de points dans les cristaux.
En A de la figure 6.14, un motif est absent : il existe au sein du cristal une lacune. La lacune d’un cation s’accompagne souvent d’une lacune d’un anion. Ces lacunes de type anion-cation s’appellent des défauts de SCHOTTKY. Elles préservent la neutralité du cristal. Leur formation demande relativement peu d’énergie.
Une lacune d’un anion dans un cristal, crée un défaut de charge(s) négative(s). Ce défaut se corrige très rapidement par la présence d’électrons libres qui se logent dans les interstices. Ce type de défaut a souvent pour conséquence de colorer le cristal. Ce type d’imperfection est dit de type F, du mot allemand Fabre qui signifie couleur.
En B de la même figure, on observe la présence d’un motif du réseau dans une zone interstitielle. S’il s’agit d’un ion, ce déplacement d’un ion du motif du réseau vers une zone interstitielle préserve la neutralité du réseau et se nome un défaut de FRENKEL. Ce type de déplacement est d’autant plus facile (demande d’autant moins d’énergie) que les interstices sont importantes. Par exemple, c’est le cas du déplacement d’un cation petit dans réseau ionique où les anions sont gros.
En C, on observe la présence d’une impureté de substitution. Un motif est remplacé par un autre. Par exemple, s’il s’agit d’un cristal métallique, un atome de zinc remplace est un atome de cuivre. On entre là dans le cas des solutions métalliques solides. S’il s’agit d’un réseau ionique, comme par exemple le chlorure de sodium, la substitution d’un ion chlorure par un ion fluorure sera sans effet sur la neutralité du cristal. Si la substitution implique in anion de charge différente, la neutralité du cristal exige qu’un cation de charge équivalente vienne substituer un cation du réseau original. Ces cas seront détaillés dans le cours de thermodynamique, chapitre XI.
En D toujours de la figure 6.14, il y a insertion d’un nouveau motif dans un interstice du cristal. Cette insertion est d’autant plus favorable que les dimensions de l’interstice et du nouveau motif sont comparables.
Il existe plusieurs composés appelés non stœchiométriques. Alors que l’oxyde de nickel, NiO, contient autant d’ions Ni++ que d’ions O- -, lorsqu’il est préparé dans un excès d’oxygène, il acquiert la formule Ni0,97O1,0. Si NiO est vert pâle et pas conducteur de l’électricité, le composé Ni0,97O1,0 est noir et est semi-conducteur. Le déficit en ions Ni++ est compensé par la présence d’ions Ni+++ pour maintenir la neutralité électrique. En outre, un électron peut sauter d’un ion Ni++ vers un ion Ni+++ et ainsi de proche en proche ce qui explique le caractère semi conducteur du composé non stœchiométrique.
3.2. Les défauts de ligne
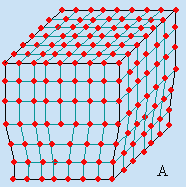
La figure 6.15 montre ce qu’on appelle la dislocation coin (A) et la dislocation vis (B).
 |
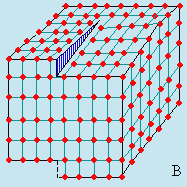 |
Figure 6.15. Dislocations coin (A) et vis (B) dans les cristaux.
Dans la dislocation coin il y a un plan de motifs qui s’insère comme un coin dans une bûche. Le réseau se dilate dans la partie concernée pour laisser l’espace nécessaire à ce plan partiel. La dislocation vis est caractérisée par le fait qu’une partie d’un plan de motifs est déformée, s’est déplacée d’un ou de plusieurs motifs par rapport au plan voisin. Au voisinage de la déchirure, le réseau est soumis à une force de cisaillement.
Ces dislocations ont des conséquences mécaniques importantes. Si on calcule pour un cristal parfait la force nécessaire pour faire glisser un plan par rapport à un autre il faut compter sur des forces de l’ordre de 109 newtons. La force réellement requise est plutôt de l’ordre de 106 newtons. Cette facilité relative est principalement due à la présence de dislocation coin. Si l’on frappe sur la partie latérale supérieure droite de la structure décrite en 6.15A, le plan partiel responsable de la dislocation se déplace vers la gauche (Fig. 6.16).
|
|
Figure 6.16. Déplacement latéral d’une partie d’un cristal sous l’effet d’une force de cisaillement : effet de la dislocation coin.
3.3. Les défauts de plan
Bien qu’ils ne constituent pas vraiment des défauts internes au cristal, les défauts de plan sont associés aux ensembles polycristallins. En effet, les cristaux sont souvent constitués d’un enchevêtrement de plusieurs cristaux. Le plan de motifs situé en surface d’un cristal contigu à un autre cristal détermine une ligne de contact au long de laquelle l’environnement électronique des motifs est différent de celui que ces motifs retrouvent à la surface du cristal.
Ce ne sont pas vraiment des défauts du cristal, mais une conséquence de l’enchevêtrement polycristallin. Les zones de raccordement de deux cristaux d’orientation différente sont appelées joints de grain. Ces régions tout comme celles situées le long d’une dislocation vis ont des propriétés particulières (Fig. 6.17). Parfois, ce sont ces régions « défectueuses » des cristaux qui leur confèrent des propriétés particulières, entre autres en catalyse.
|
|
Figure
6.17. Polycristaux de NaCl.
Source :
http://www.rsc.org/pdf/molecularworld/third_dimension_intro.pdf
Malheureusement cette source ne semble plus disponible 2014-12-18.
4. Autres arrangements
d’atomes à l’état solide
On vient de le voir, l’état cristallin possède un très haut niveau d’arrangement périodique dans l’espace : le motif se répète systématiquement sur un axe. Ce n’est cependant pas toujours le cas. Il existe d’autres modes d’organisation, dont celui où il y a absence complète d’organisation : c’est l’état amorphe. Il existe un état intermédiaire appelé l’état vitreux. Cet état correspond en quelle que sorte à l’état liquide « gelé ».
5. Les propriétés
thermiques des solides
La théorie de la capacité calorifique des solides est complexe et hors d’atteinte de ce premier cours de chimie universitaire. Disons que, comme son nom l’indique, la capacité calorifique veut mesurer la capacité qu’un constituant a d’emmagasiner de l’énergie. Plus précisément, on veut connaître la quantité d’énergie que le constituant, dans le cas présent un solide, peut accumuler. Bien évidemment, la quantité de matière est importante. Si on double la quantité, on double très certainement sa capacité calorifique. On retiendra donc une quantité unitaire de matière. Plutôt que le kilogramme, on retiendra la mole, ce qui permet de mieux comparer un composé chimique à un autre.
Cette capacité calorifique dépend aussi de la température, de la pression et éventuellement du volume du composé. Sans entrer plus profondément dans ces considérations, on mesurera la capacité calorifique à volume constant Cv. On retiendra le kelvin comme unité de température et on déterminera, par exemple, la quantité d’énergie accumulée par une mole de constituant lorsqu’on élève sa température de 1 K.
On le verra en détail dans un cours de chimie théorique, mais disons seulement qu’un solide ne peut emmagasiner de l’énergie que dans son réseau cristallin sous la forme d’énergie de vibration. Les atomes ou les ions constituant le réseau cristallin ont la possibilité autour de leur position d’équilibre. Plus la température est élevée et plus les atomes, les ions, les molécules,… vibrent.
La première observation systémique est traduite dans la loi de DULONG et PETIT :
La capacité calorifique d’un solide monoatomique est de 3 R (6 cal/mol ou 25 J/mol). R est la constante des gaz parfaits. On peut aussi dire que cette capacité calorifique est de 3 k par atome (k est la constante de BOLTZMANN).
Cette loi est générale et valides à la température ambiante. Il existe une exception notoire : la carbone. En fait, si l’on trace le graphe de la capacité calorifique molaire à volume constant en fonction de la température, on observe que cette fonction a une forme sigmoïde et que la valeur de la capacité calorifique molaire du carbone atteint bien 25 J/mol à plus haute température (Fig. 6.18).
|
|
Figure 6.18. Variation de la capacité calorifique molaire à volume constant du cuivre et du carbone.
Ainsi à la température du zéro absolu, la capacité calorifique des solides monoatomiques est nulle. Cette observation est aussi vraie pour les solides poly atomiques. En d’autres termes, tout se passe comme si le réseau cristallin arrête complètement de vibrer au zéro absolu. Plus la température croît et plus le solide accumule de l’énergie pour finalement tendre vers une sorte de saturation qui correspond à la valeur de 25 J/mol (Tableau 6.8).
Pour les solides poly atomiques, la même loi est encore valide pourvu que l’on multiplie la valeur correspondant à la saturation observée pour les solides monoatomiques par le nombre d’atomes constituant le solide. Ainsi, pour les oxydes CuO, MnO, MgO,… la valeur limite sera voisine de 50 J/mol. Et ainsi de suite pour les solides tri, tétra atomiques…
On note aussi que le comportement en fonction de la température est le même : on retrouve chaque fois la courbe en forme de S pour la variation de la capacité calorifique en fonction de la température. Le tableau 6.8 montre bien que l’augmentation de température de 300 à 800 K permet d’atteindre ou même de dépasser la valeur formulée par la loi de DULONG et PETIT. Un bon exemple est celui de l’oxyde de chrome à 800 K, sa capacité calorifique molaire est bien égale à 5 fois celle d’un solide monoatomique.
Tableau 6.8. Capacités calorifiques* de quelques solides
| Solide | Cv (300 K) | Cv (800 K) | Solide | Cv (300 K) | Cv (800 K) |
| Ag | 25,5 | 28,0 | CuO | 46,0 | 53,9 |
| Al | 24,2 | 30,5 | FeO | 50,6 | 54,3 |
| Cr | 24,2 | 28,8 | MgO | 37,6 | 48,1 |
| Cu | 24,2 | 27,6 | ZnO | 44,7 | 50,6 |
| Fe | 24,7 | 37,2 | Ag2S | 75,2 | 90,3 |
| Mg | 23,8 | 30,5 | SiO2 | 56,0 | 71,5 |
| P | 23,8 | - | Al2O3 | 83,6 | 120,4 |
| Pb | 27,2 | - | Cr2O3 | 110,4 | 125,0 |
| Zn | 25,2 | - | * : en J/(mol) | ||
En considérant qu’à zéro degré absolu, le réseau peut vibrer à une fréquence comprise entre 0 et nm, DEBYE a élaboré une théorie qui montre qu’aux très basses températures, la capacité calorifique molaire à volume constant est donnée par la relation :
| 6.1 |
|
N est le nombre d’AVOGADRO, k est la constante de BOLTZMANN et qD une constante caractéristique du solide appelée la température caractéristique de DEBYE. Elle à la valeur du rapport hnm/ k.
Ainsi à très basse température la capacité calorifique est de la forme :
| 6.2 |
Cv = a T3 (Fig. 6.19). |
|
|
Figure 6.19. Variation de la capacité calorifique molaire à volume constant du cuivre et du carbone.
Une théorie plus générale a été élaborée par EINSTEIN. Ce dernier, en considérant les modes de vibration des atomes autour de leur position d’équilibre, a pu relier la capacité calorifique à la fréquence n de ces vibrations. Il a obtenu la relation suivante :
| 6.3 |
|
N et k ont la même signification que dans l’équation de DEBYE et h est la constante de PLANCK. C'est l'équation générale d'EINSTEIN. On pose qE = hn / k.
qE s’appelle la température caractéristique de EINSTEIN pour le solide considéré. Le tableau 6.9 montre que les températures caractéristiques de DEBYE et d’EINSTEIN ont beaucoup de ressemblances de même qu’avec celles calculées à partir de l’élasticité des solides.
Tableau 6.9. Températures caractéristiques (K) de DEBYE et d’EINSTEIN pour quelques éléments
| Substance |
qD a | qE b | qS c |
| C (diamant) | 2200 d – 2300 e | 1840 | -- |
| sodium | -- - -- | 159 | -- |
| aluminium | 385 - 426 | 398 | 399 |
| potassium | -- - -- | 99 | -- |
| fer | 428 - 464 | 420 | 467 |
| cuivre | 331 - 344,5 | 315 | -- |
| zinc | 205 - 300 | 235 | -- |
| molybdène | 379 - 440 | 379 | -- |
| argent | -- - 225 | 215 | 212 |
| cadmium | 129 - 186 | 160 | 168 |
| étain | 127 - -- | 160 | -- |
| platine | 240 - -- | 225 | 226 |
| or | 162 - 165 | 180 | -- |
| plomb | 96 - -- | 88 | 72 |
| a : équation
de DEBYE (basse température) ; b : équation générale d’EINSTEIN 6.2; c : Calculées à partir des constantes d’élasticité des solides ; d : valeurs tirées du Handbuch der experimental physik – tableau XIV-2, Vol. 8 (Eucken) ; e : valeurs tirées du Handbook of chemistry, 50e édition, page D-129. |
|||
6. Relation entre la
structure d’un composé et le point de fusion
Il n’existe pas de règle générale permettant de relier la nature d’un composé et sa température de fusion. On peut cependant considérer quelques éléments que sont la symétrie, la présence (ou l’absence) de groupes polaires et à l’intérieur d’une famille de composés apparentés la masse moléculaire totale.
Plus un composé est symétrique et plus sa température de fusion est élevée. Le cas du carbone diamant et du carbone graphite est un bon exemple de la précédente affirmation.
Dans une série de composés appartenant à une même famille, par exemple les alcane linéaires, on s’attend à ce que la température de fusion croisse en fonction de la masse moléculaire. La figure 6.20 montre la pertinence d’une telle remarque. Elle montre en outre un détail intriguant que, hormis le cas du méthane et de l’éthane, les alcanes semblent s’organiser en deux groupes : les alcanes à nombre de carbone pair et ceux à nombre de carbone impair. Le groupe des alcanes linéaires à nombre de carbone pair ont une température de fusion quelque peu supérieur à celle des alcanes à nombre de carbone impair même si de manière systématique l’ajout d’un groupe CH2 augment la température de fusion.
|
|
Figure 6.20. Température de fusion des alcanes linéaires.
La série des diacides organiques HOOC-(CH2)n-COOH, donc à chaîne linéaire, montre une progression de la température de fusion qui est encore plus déroutante : la température de fusion de ces homologues temps à décroître pour les valeurs de du nombre d’atomes de carbone n allant de 0 à 16. En fait, les températures s’arrangent en deux groupes selon que n est pair ou impair : les diacides à nombre impair de carbone ont une température de fusion de plusieurs dizaines de degrés inférieure à ceux des diacides à nombre impair d’atomes de carbone (Fig. 6.21).
|
|
Figure 6.21. Température de fusion des diacides linéaires.
Cette série de molécules est formée de structures qui sont terminées par des groupes fortement polaires. L’orientation relative de ces groupes polaires entre les molécules permet de créer au sein du solide cristallin des interactions attractives fortes dans la série des diacides à nombre d’atomes de carbone pair. L’apport d’énergie doit donc être plus important pour rompre ces interactions. Ces interactions doivent être beaucoup plus faibles dans le cas des diacides à nombre de carbone impair, expliquant du même coup leur plus faible température de fusion.
Les composés organiques quelque peu complexe ont la propriété de se décomposer avant que leur température n’atteigne leur point de fusion. Afin de les caractériser, on ne peut donc mesurer leur point de fusion. En alternative, on peut parfois mesurer leur température de fusion lorsqu’il sont immergés dans l’eau. Il s’agit d’un test de fusion sous eau (Fig. 6.22). Bien entendu le composé doit être non miscible dans l’eau. C’est le cas de l’acide benzoïque qui a une température de fusion sous eau de 94 ºC alors que la température de fusion normale est de 121,7 ºC. De la même manière, l’acétanilide à une température de fusion sous eau est de 83 ºC et sa température de fusion normale de 114 ºC.
|
|
Figure 6.22. Mesure du point intertectique.
Autre variante : le point de fusion semitectique. Plusieurs composés ont la propriété d’incorporer des molécules d’eau. Par exemple, plusieurs sels anhydres ont cette particularité d’incorporer dans leur structure cristalline des molécules d’eau :
Sel anhydre + eau ® sel hydraté (insoluble dans l’eau)
L’exemple est celui de la codéine (3-morphine méthyle éther). Le point de fusion de la codéine pure est de 165 °C alors que celui de la codéine hydratée sous eau est de 65 °C. On appelle ce point de fusion le point semitectique.
8. Les
propriétés mécaniques du solide
L’état solide ne se réduit pas à un système cristallin unique ou encore à un état amorphe. Le plus souvent un solide apparaît formé d’une multitude de micro cristaux. L’observation des surfaces de ces solides à l’aide de microscopes éclairés en lumière polarisée produit des images souvent spectaculaires.
8.1.
Le module d’YOUNG
Parmi les propriétés mécaniques fréquemment mesurées, mentionnons l’étirement sous contrainte avec la détermination du module d’YOUNG.
Lorsqu'une contrainte est appliquée à un matériau de longueur l, par exemple une force F, visant l'étirement, la résultante, ici l'étirement Dl, est proportionnel à cette contrainte (Fig. 6.23). La contrainte éliminée, le matériau reprend sa longueur initiale. Cette constante est le module d'Young. Le module d'Young est la contrainte qui produit un allongement de 100 % de la longueur initiale (Tableau 6.10). Bien évidemment, les matériaux se déforment de manière permanente, ou même se casse, pour des allongements beaucoup plus faibles. Note:voir ci-dessous la figure 6.25.
 |
Figure 6.23. Effet d’une force sur l’allongement d’un matériau.
| 6.4 |
|
Tableau 6.10. Quelques modules d'Young E
| Matériaux |
Module d'Young |
Matériaux |
Module d'Young |
| Nanotubes (C) | 1 100 000 | Soie d'araignée | 60 000 |
| Diamant | 1 050 000 | Bois de chêne | 12 000 |
| Mo | 329 000 | Nylon | 2 000 - 4 000 |
| Acier (18-10) | 203 000 | Polyéthylène | 200 - 700 |
| Verre | 69 000 | Cheveu | 10 000 |
| Granite | 60 000 | Cartilage | 24 |
| Plexiglass | 2 380 | Collagène | 6 |
8.2. Les essais de dureté
Chronologiquement, l’une des premières mesures (il s’agit plutôt d’une classification) de la dureté d’un solide a été proposée en 1822 par un minéralogiste allemand du nom de MOHS. Il proposât une échelle graduée de 1 (pour les solides les plus faciles à rayer) à 10 (pour les solides les plus résistants à la rayure, en l’occurrence le diamant). Cette méthode est approximative et ne permet pas certaines distinctions comme par exemple pour les agrégats friables. Si l’ocre rouge se raie à l’ongle, il est formé de grains fins d’hématite qui raient le verre. La production de matériaux modernes ne s’accommode pas d’une telle échelle.
Tableau 6.11. La classification de dureté de MOHShttps://www.mindat.org/min-859.html
| Dureté | Minéral | Commentaires | Exemples |
| 1 |
talc |
très facile à rayer avec l’ongle | 0,5-1 : graphite |
| 2 | gypse |
2,2 : ongle | |
| 3 |
calcite |
se raye avec le cuivre | 3,2 : cuivre |
| 4 |
fluorite |
||
| 5 |
apatite |
se raye par le verre | 5,1 : lame de couteau |
| 6 |
orthoclase |
se raye par l'acier | 6,5 : aiguille d’acier |
| 7 |
quartz |
raye une lame de couteau | 7,0 : Si polycristallin |
| 8 | topaze |
||
| 9 |
corindon |
9,5 : bore fondu à l’arc | |
| 10 | diamant |
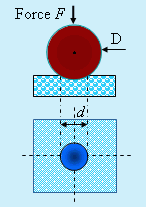
L’essai de dureté moderne mesure la résistance d’une surface solide à la pénétration, l’intrusion, d’un objet particulier. La dureté se mesure à travers l’importance d’une déformation introduite par un objet pointu lui-même soumis à une force dirigée perpendiculairement sur la surface du solide. Il existe plusieurs méthodes de mesures. Notons trois techniques qui se différencient par la géométrie du corps qu’on essaie d’introduire dans le matériau (Tableau 6.12) (Fig. 6.23A et 23B). Les méthodes Brinell et Vickers produisent essentiellement les mêmes résultats.
Tableau 6.12. Géométrie des objets utilisés pour la mesure de dureté
|
Méthode de
mesure |
Géométrie de l’objet à faire pénétrer : l'indenteur |
| BRINELL | une sphère en acier trempé, en carbure de tungstène et de 10 mm de diamètre. |
| VICKERS |
une pyramide en diamant de base carrée et de 136° d’angle d’ouverture |
| ROCKWELL (type C) | une pyramide de base carrée et 120° d’angle d’ouverture |
| KNOOP | une pyramide de base en forme de losange avec différents angles, par exemple, 130° dans un sens et 172,5° perpendiculairement |
 |
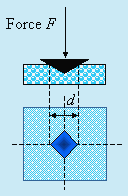 |
|
| A : essai de dureté BRINELL | B : essai de dureté VICKERS |
Figures 6.23. Essais de dureté BRINELL et VICKERS.
La norme BRINELL (1849-1925) a été éditée dès 1924. La charge appliquée est comprise entre 5 000 et 30 000 N (500 et 3 000 kg). La pression est maintenue pendant 15 à 30 s selon le solide. Si la force F est exprimée en kgf, le diamètre de l'empreinte d en mm, la dureté Brinell HB (N/mm2) est calculée à l'aide de la formule suivante :
|
HB = |
|
Comme la mesure de dureté BRINELL peut être réalisée dans diverses conditions, une manière convenable de présenter les résultats est devenue courante. Elle est de la forme :
150 HB 10/500/15
Cela signifie que la dureté BRINELL d’un matériau est de 150 obtenue avec une bille de 10 mm de diamètre, avec un poids de 500 kg maintenue pendant 15 s. Note : attention aux unités. Dans le système international, l’unité de dureté s’exprime en N/m2. On voit aussi l’écriture suivante HB (3000) : la dureté est mesurée avec une force de 3 000 kg. Puisqu’il y a une relation entre la grandeur de l’empreinte, le diamètre de la bille et la force appliquée, on considère que pour être valable, la mesure de l’empreinte sur la surface du solide, d, doit être comprise entre 2,5 et 4,75 mm. L’échelle dureté BRINELL convenable se situe entre 80 et 445 pour cette force.
La norme Vickers, du nom de la compagnie anglaise où cette méthode a été mise au point, a été adoptée en 1952. La charge appliquée, de 10 à 1200 N (1 à 120 kg), est appliquée pendant 15 s. L’empreinte est de l’ordre de la fraction de mm : elle est mesurée à l’aide d’un microscope. La dureté Vickers, HV, est obtenue par la formule suivante :
|
HV = |
|
Note : d est la diagonale en mm de l’empreinte carrée et la force F est exprimée en kg (Fig. 6.23B). La présentation correcte de la dureté Vickers est de la forme
600 HV /20 /15
Ce qui signifie une dureté de 600 obtenue avec une force de 20 kg pendant 15 s. À nouveau, attention à l’expression des unités pas toujours très rationnelle dans ce secteur d’activités, les techniciens utilisent le plus souvent le kg et le mm2, les universitaires de leur côté utilisent le système international, donc le N et le m2.On a vu plus haut, paragraphe 2.2, que les composés uniaxes et bi-axiaux ont des propriétés physiques qui diffèrent selon l'axe d'observation. Il en est de même de la dureté. Par exemple, le rubis utilisé industriellement présente une dureté pouvant varier de près de 50 % selon l'axe d'observation.
Tableau 6.13A. Dureté de quelques bois pour plancher
| Essences de bois |
Dureté
Brinell (N/mm2) |
| Bambou | 4 |
| Châtaigner | 1,5 à 2,3 |
| Chêne | 2,8 à 4,2 |
| Érable | 3,1 |
| Merisier | 2,9 à 3,1 |
| Pin | 1,2 à 2 |
Tableau 6.13B. Quelques valeurs de dureté de métaux
| Métal | Dureté Vickers | Métal | Dureté Vickers |
| Al | 35-48 | Os | 670-1000 |
| Be | 200 | Ta | 200 |
| Cr | 220 |
W | 500 |
| Co | 320 |
U | 250 |
| Cu | 87 |
V | 150 |
8.3.
L’essai de résilience
L’essai de résilience est effectué à l’aide d’un appareil de type pendule appelé «mouton pendule» ou «mouton de CHARPY» (1865-1945). Le pendule, laissé à lui-même, tombe d’une hauteur H sur un échantillon (éprouvette). Il le (la) casse et poursuit son mouvement pendulaire pour remonter jusqu’à une hauteur h. La perte d’énergie du pendule utilisée pour briser l’échantillon, mesurée à travers la différence H – h, s’appelle la «résilience» (Fig. 6.23). La résilience K est mesurée à travers la relation suivante (g est l’accélération de la pesanteur: 9,807 m s-2) :
K = M g (H – h)
L’éprouvette est constituée d’une tige de section carrée entaillée en forme de V ou de U avec des dimensions standardisées. Le couteau a lui aussi des dimensions et une masse M également standardisées.
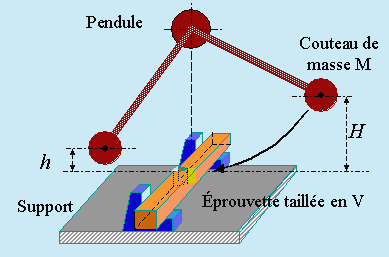 |
Figures
6.23. Essais de résilience.
Voir
une brève animation dans le chapitre présenté en PowerPoint: diapositive 52.
8.4.
L'essai de traction
Dans ce cas, l'appareil est dans le principe similaire à celui utilisé pour la mesure du module d'YOUNG. L’éprouvette a une forme de H. Elle est solidement attachée dans les mâchoires de deux pièces, l’une est fixe, l’autre est mobile. Cette dernière sert à tirer sur l’échantillon à l’aide d’une force F. On mesure simultanément cette force et l’allongement de l’échantillon à l’aide d’un extensomètre (Fig. 6.24).
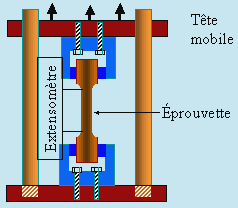 |
Figures 6.24. L'essai de traction.
La figure qui suit montre la contrainte nécessaire pour une déformation souhaitée de l'échantillon solide. Cette variation n'est pas linéaire. Pour de faibles contraintes, vers l'origine, la pente à la courbe est simplement le module d'YOUNG.
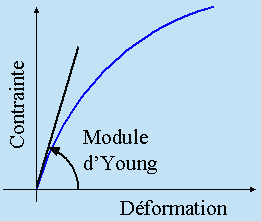 |
Figure 6.25. L'essai de traction.
8.5. Le
fluage
9. Les quasi cristaux
Dans un système
Référence :
http://www.radio-canada.ca/nouvelles/science/2011/10/05/001-nobel-chimie-shechtman.shtml
On trouvera d'excellentes images de ce que peut être une structure de quasi cristaux à l'adresse internet précédente ainsi qu'à:
10. Conclusions
|
Alors qu’à l’état liquide ces atomes ou molécules peuvent se mouvoir et glisser les unes sur les autres, dans le solide elles sont figées le plus souvent dans un arrangement tridimensionnel périodique. Si ce réseau a les mêmes propriétés dans les trois directions du trièdre trirectangle, le solide est isotrope. Dans le cas contraire il est anisotrope : ses propriétés varient selon l’angle d’observation. En outre, si les liquides et encore plus les gaz peuvent absorber de l’énergie à travers les déplacements (énergie cinétique) des atomes ou des molécules, la phase solide n’accumule de l’énergie qu’à travers la vibration des atomes et des molécules dans le réseau tridimensionnel (énergie de vibration).
|
Le Handbook of Chemistry and Physics, CRC Press, contient une grande variété et quantité d’informations très utile au chimiste. Ainsi, on trouve dans la 70e édition, 1989-1990, les tables suivantes :
| Nom de la table | Description sommaire | pages |
| Coefficient de dilatation thermique linéaire | Valeurs pour une trentaine de métaux à 25 °C | D-187 |
| Liquides pour la méthode par immersion | Une vingtaine de liquides dont l’indice va de 1,45 à 2,06 | E-379 |
Liens utiles
sur le Web :
Le lecteur trouvera de nombreux sites sur le web tant en français qu’en anglais.
David N.
Blauch, Collège Davidson, Caroline du Nord, propose
une description de plusieurs expériences relatives à des mesures de
calorimétrie en effectuant des mesures virtuelles sur le site :
http://www.chm.davidson.edu/ChemistryApplets/calorimetry/index.html
(visité le 2019-02-12).
La biographie de CHARPY ainsi que des explications sont aussi disponibles (M. A Papineau, prof., École des Mines de Paris) : http://www.annales.org/archives/x/charpy.html (visité le 2019-02-12).
En anglais, plusieurs sites web sont accessibles. Un
site anglais est très explicatif sir les différentes méthodes de mesure de
dureté :
http://www.gordonengland.co.uk/hardness/
Un site en français qui montre une panoplie d'appareils de mesure. On y trouve entres autres la mesure de l'empreinte Brinell déjà disponible en 1925.
Et encore: https://fr.wikipedia.org/wiki/%C3%89chelle_de_Mohs ainsi que les références que l'on trouvera en bas de la page sur les différentes méthodes de mesures de dureté (visité le 2019-02-12).
La dureté des éléments (ainsi que de nombreuses autres propriétés) exprimée à travers un tableau périodique est également disponible. La navigation sur le site est un peu compliquée. On résout le problème en indiquant un élément quelconque à la fin de l’adresse. Ici, on a choisi le bore /B/. Cela ouvre une fenêtre dans laquelle on choisit la propriété recherchée :
http://www.webelements.com/webelements/elements/text/B/ (visité le 2015-12-29).Pour la relation entre l'indice de réfraction et la densité, voir:
http://www.geowiki.fr/index.php?title=Compl%C3%A9ments_sur_la_duret%C3%A9%2C_la_densit%C3%A9_et_l'indice_de_r%C3%A9fraction (visité le 2019-02-12).
On trouve de nombreuses informations sur les cristaux à l'adresse : https://www.mindat.org/ (visité le 2019-02-12).
Problème Nº 1
Le chlorure de césium a une densité de 3,97 kg/dm3 et cristallise dans le système cubique centré. Le motif (le cube) a un côté de 0,412 nm et contient l’équivalent d’une molécule CsCl. Calculez la valeur du nombre d’Avogadro.
Réponse
: N
= 6,0639 10+23
Problème Nº 2
Le tungstène cristallise dans le système cubique centré dont le côté du cube mesure 0,316 nm. Combien il y a t’il d’atomes de tungstène par unité cubique ? Quelle est la masse volumique de ce métal ?
Réponse
: masse
volumique
= 19 348 kg/m3
Problème Nº 3 Masse moléculaire
Un composé inconnu a une densité de 4,56 t/m3. Il cristallise dans le système quadratique dont la maille élémentaire à les dimensions suivantes : a = b = 0,658 nm et c = 0,593 nm. Si la maille élémentaire contient quatre molécules, calculez la masse moléculaire de ce composé.
Réponse : M = 176,3 g/mole.
Problème Nº
La densité du fluorure de calcium, CaF2, est de 3 180 kg/m3 à 20 °C. Calculez la dimension du cube qui contient quatre ions Ca++.
Réponse : l = 0,5464 nm
Problème Nº 5 Le fer
À 1425 °C le fer cristallise dans le système cubique centré dont le côté de la maille élémentaire est de 0,293 nm. En supposant que la structure est la plus compacte possible, calculez :
1- le rayon de l’atome de fer ;
2- la distance entre deux atomes de fer les plus proches ;
3- le nombre d’atomes de fer par maille élémentaire ;
4- le volume occupé par un atome de fer ; et
5- la portion de volume du solide inoccupée.
Réponse : f
= 67,9 %
Problème Nº 6 Loi de Debye
La capacité calorifique d’un métal est de 1,63 J/(K mole) à 20 K.
1- Calculez la constante a de la loi simplifiée de DEBYE à basses températures.
2- Calculez la capacité calorifique du même métal à 5 K.
3- Calculez la Température caractéristique de DEBYE.
Réponse
: qD = 212 K
Dernière mise à jour : 2019-02-12.
x x x x x x x x x x x x