CHAPITRE 4

L’état liquide (1)

1.  Les propriétés mesurables

On a vu que les lois du gaz idéal font place aux lois des gaz non idéaux dès que la température diminue et que la pression croît.  En fait, l’écart à l’idéalité s’accroît d’autant plus que la matière se rapproche de son point de liquéfaction.  La loi de VAN DER WAALS donne un bon exemple de ce comportement.

L’application des lois du gaz non idéal ne s’appliquent plus.  La théorisation de l’état liquide est encore possible ; elle est cependant hors d’atteinte pour le niveau de ce cours.  On se contentera plutôt d’exposer les propriétés mesurables, donc observables.

Ces propriétés sont nombreuses et variées.  Il existe plusieurs manières de classer ces propriétés.  Par exemple, certaines mesures requièrent la destruction de l’échantillon : d’autres pas.  Ce peut être un avantage d’utiliser un essai non destructif car alors, l’intégrité de l’échantillon étant maintenue il est encore disponible pour un autre type de mesure. 

Certaines propriétés sont dites extensives.  Dans ce cas la propriété ne dépend pas de la quantité de matière.  L’indice de réfraction d’un liquide est au nombre de cette catégorie.  Par opposition, d’autres propriétés sont dites intensives : elles dépendent de la quantité de matière.  C’est le cas bien évidemment de la masse d’une substance.

Nous les classifierons sous quatre rubriques relativement simples et quelque peu arbitraires que l’on étudiera successivement.  Certaines de ces propriétés sont :

1-     Les propriétés physiques.

a.       La densité et la masse volumique ;

b.      La viscosité ;

c.       La mesure des points de congélation et d’ébullition, auxquels points on ajoutera les points triple et critique des liquides (ce dernier ayant été vu au chapitre précédent..

2-     Les propriétés optiques.

a.       L’indice de réfraction ;

b.      La polarimétrie ;

c.       L’absorptiométrie sous ses différentes formes.

3-     Les propriétés électriques et diélectriques.

a.       Le moment dipolaire ;

b.      La constante diélectrique

c.       L’indice de réfraction déjà classé dans les propriétés optiques.

4-     Les propriétés thermiques.

a.       Les diverses capacités calorifiques ou chaleurs latentes ;

b.      …

Les propriétés optiques et électriques seront abordées dans le chapitre 5.

Ces propriétés ne sont pas nécessairement uniquement propres aux liquides.  Bien sûr elles sont bien souvent d’applications générales.  Un gaz, un liquide ou un solide pur ont une capacité calorifique molaire à volume constant.  Il en est de même de l’indice de réfraction.  On verra par contre que les solides ont par définition une viscosité infinie.  Cette propriété se limite donc aux gaz et aux solides.  Ce chapitre sortira donc à l’occasion du substrat liquide pour compléter certaines informations, ajouter des particularités relatives à l’état gazeux et à l’état solide.

2. Les propriétés physiques

2.1.      La mesure de la densité

La densité s’exprimait le plus généralement et le plus simplement en g/cm³ dans l’ancien système d’unités CGS.  En SI, cette même valeur s’exprimerait en kg/m³.   Ainsi pour l’eau pure, sa densité est d’environ 1 g/cm³  ou 1 000 kg/m³.  On a ici un exemple de l’intérêt de l’usage du système CGS, système dont on décourage maintenant l’usage.  En SI, on appelle cette ancienne notion par masse volumique.  On ne parlera pas ou peu de la méthode de mesure.  Il est cependant plus qu’utile de revenir sur certains aspects de cette propriété.

2.1.1. La densité

Il existe plusieurs sites web que l’on pourra consulter (voir à la fin de ce chapitre).  Rappelons seulement la définition de la densité : c’est un nombre sans dimension égale au rapport d'une masse d'une substance à celle de l'eau pure occupant un même volume à 3,98 °C.  Cette définition suppose bien sûr que la substance soit homogène.  Par définition, la densité de l’eau à 3,98 °C est égale 1.  L’intérêt évident de cette définition de la densité est de s’affranchir d’un système d’unités. 

L’établissement de la densité repose donc sur deux types de manipulation : la mesure d’une masse et d’un volume.  Dépendamment de la précision recherchée, les techniques utilisées peuvent varier profondément.  L’obtention d’une mesure à ± 5 % ou encore à une décimale près ne demande évidemment pas le même soin qu’une valeur à ± 0,1 % ou encore à la troisième décimale près.

Une première approche simple consiste à utiliser des densimètres.  Ces appareils ressemblent physiquement à des thermomètres dans lesquels le réservoir de mercure a été remplacé par un réservoir de lest.  Plongé dans un liquide dont on veut connaître la densité, il s’y enfonce jusqu’à ce que la loi d’Archimède soit satisfaite : la masse du densimètre étant alors égale à la masse du volume du liquide déplacé.  Dépendamment du soin apporté à la graduation du densimètre, ces appareils sont vendus pour travailler dans des plages de densité allant par exemple de 850 à 1 000 kg/m³ (0,85 à 1,00 g/cm³) avec une imprécision au moins égale à  ± 0,05.

Les mesures plus précises sont réalisées en mesurant la masse d’un volume connu.  La précision du résultat dépendra bien entendu de la précision avec laquelle sont obtenues les deux valeurs précédentes.  Avec de bons instruments, on peut obtenir aisément des résultats à 0,001 %.

Comme le volume d’une substance varie avec la température, il en est de même de sa densité.  

Sans entrer dans le détail, le terme "densité" se traduit en anglais par l’expression "specific gravity".

2.1.2. La densité relative

La densité relative s’exprime encore par un nombre sans dimension.  C’est le rapport entre une masse volumique et la masse volumique de l’eau  dans des conditions spécifiées mais quelconque de températures.  La densité relative constitue donc  en quelque sorte une extension de la densité.  On l'exprime souvent sous la forme :

Dans cette expression T₂ et T₁ représentent les températures de mesure des masses volumiques de la substance et de l’eau, respectivement.  L'expression anglaise équivalente est "relative density".

2.1.3. La masse volumique

C'est, pour une substance homogène, le rapport entre sa masse et le volume qu'elle occupe.  La masse volumique s'exprime en kg/m³ dans le système international d'unités.  Ainsi la masse volumique de l’eau pure à 4 °C est de 999,973 kg/m³.

  2.1.4.  L'effet de la température

Lorsqu’ils sont soumis à une élévation de température, les molécules accumulent de l’énergie sous forme cinétique (le mouvement de translation) et de rotation : les liquides augmentent de volume.  L’accumulation d’énergie avec la température augmente l’importance du mouvement brownien.  Il en résulte une dilatation du volume.  On dira que le liquide possède un coefficient de dilatation thermique.  Ce coefficient a exprime l’augmentation D V d’un volume V pour une élévation de 1 °.  Ou encore :

Ce coefficient s’exprime comme l’inverse d’une température (°C^-1) ou encore en utilisant l’échelle absolue de température K^-1.  Cette définition du coefficient de dilatation thermique est similaire à celle du coefficient de dilatation linéaire à ceci près que la mesure est faite sur un volume, en trois dimensions, et non plus dans une seule direction.  On l’appelle aussi pour cette raison le coefficient de dilatation cubique.  L’augmentation d’un certain volume V’ de liquide soumis à une élévation de température DT’ se déduit de la formule précédente :

DV   =  a V’ DT’

 Tableau 4.1.  Quelques coefficients de dilatation volumique de liquides au voisinage de 20 °C en K^-1

Il faut aussi ajouter que le coefficient de dilatation volumique varie aussi avec la température.  L’augmentation de volume n’est donc pas une fonction linéaire de la température.  On observe généralement une augmentation de plus en plus rapide du volume d’un échantillon lorsque la température augmente.  Sur la figure qui suit, on remarque cette tendance ainsi que le minimum bien connu du volume de l’eau vers 4 °C.  L’équivalent inverse est bien sûr le maximum de la densité de l’eau.

Figure 4.1.  Variation d’un volume d’eau liquide avec la température.

Tableau 4.2. Variation du coefficient de dilatation volumique de l’eau (× 10³) avec la température

Le liquide augmente de volume et en conséquences, comme il n’y pas variation concomitante de masse, la densité du liquide diminue lorsque la température augmente.  Le tableau et la figure qui suivent illustrent ce phénomène.

Figure 4.2.  Variation de la densité de l'eau avec la température.

Un problème mal attribué 

Dans le contexte appréhendé du réchauffement climatique, on entend à l’occasion que l’augmentation du niveau des océans est liée à la fonte des glaciers, en particulier ceux des calottes glaciaires et du Groenland.  En fait, cette augmentation ne peut en au cas provenir de la fonte de la calotte glaciaire du pôle Nord et des « icebergs ».  Ces glaces flottent sur l’eau  de mer et leur masse est égale à celui du volume d’eau déplacée.  Leur fonte complète n’augmentera pas le niveau des mers.  La situation est un peu différente des glaces qui reposent sur un continent et qui bien évidemment en fondant vont grossir le volume des océans comme cela est le cas des glaces recouvrant le Groenland.

Mais la aussi, leur contribution au volume des océans demeure limitée.  L’augmentation du niveau des océans est plutôt le résultat de l’augmentation de la température des eaux de surface des océans.  Si l’on admet que seule la couche supérieure de 1 000 m d’épaisseur est en équilibre thermique avec l’atmosphère, avec un coefficient de dilatation thermique de 2,6 × 10^-4 °C^-1 et une augmentation de 0,6 °C de la température ambiante, une colonne d’eau de 1 km, augmente d’un volume équivalent à une augmentation de hauteur de 0,156 m.  La fonte des glaces ne constitue donc pas la cause première de l’élévation du niveau des océans.

Le cas particulier de l’eau pure.

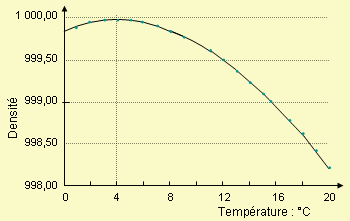
La figure 4.2 montre la variation de la densité de l’eau avec la température.  Cette  figure est explicite et montre sans ambiguïté que la densité de l’eau passe par un maximum au voisinage de 4 °C.  On a indiqué plus haut que ce maximum est atteint à 3,98 °C.  Par définition l’eau à cette température a exactement une densité de 1.  Cette figure montre en particulier tout le soin qu’il faut apporter à la mesure de la densité relative.  Elle explique aussi le phénomène de la fonte des glaces sur les lacs au printemps lorsque le lac « cale ».  La couche d’eau superficielle, lorsqu’elle atteint 4 °C devient plus dense que celle des couches inférieures.  Il s’ensuit un brusque déplacement de ces eaux de surface vers le fond du lac et une remontée des eaux moins denses et plus chaudes qui font fondre les glaces restantes.

2.1.5.  L'effet de la pression

Pour être complet, il aurait fallu préciser dans les lignes précédentes que l'effet de la température sur la masse volumique était présenté à pression constante.  On observe aussi un effet de pression à température constante similaire au précédent effet.  On doit introduire un coefficient d'expansion volumique à température constante, b, qui s'exprime comme l'inverse d'une pression, P^-1. 

On comprend aussi que les liquides tout comme les solides ont des coefficients de dilatation volumique beaucoup plus faibles que ceux rencontrés à l'état gazeux.  Cette simplification est souvent appelée "l'incompressibilité des phases condensées", sous-entendu devant celle des gaz.  Elle existe néanmoins.

2.2.            La tension de surface

a-      Explication du phénomène

Dans un liquide, on peut imaginer que les molécules qui sont à l’intérieur du liquide sont soumises à des forces différentes de celles subies par les molécules qui sont situées à la surface du liquide.  En effet, dans la phase liquide contrairement à ce que l’on a vu en phase gazeuse, les molécules se touchent.  Bien souvent, ces molécules ne sont pas neutres sur le plan électrique.  C’est le cas tout particulièrement de l’eau qui porte un moment dipolaire important.  Ces moments dipolaires interfèrent les uns avec les autres de telles sorte qu’au sein du liquide une molécule est l’objet de tensions orientées dans toutes les directions de la sphère qui l’entoure.  Sur la surface du liquide, ces tensions sont limitées à la demi-sphère située sous la surface.  Il s’ensuit que la résultante de ces forces ne doit pas être nulle (Fig. 4.3).

Figure 4.3.  Situations comparées de molécules à l’intérieur ou en surface du liquide.
A gauche le réservoir de liquide ; à droite agrandissement à l’échelle moléculaire.

Ce phénomène se traduit par l’apparition d’une tension de surface caractéristique de chacun des liquides. Visuellement parlant, on pourrait dire qu’il se forme un film de molécules en surface qui n’a pas plus tout à fait la même structure que celle que l’on retrouve au sein du liquide.

b. La capillarimétrie

Cette tension de surface se traduit en particulier dans le cas de l’eau par ce que l’on appelle la montée capillarimétrique.  En effet, sur un récipient contenant de l’eau pure, plongeons verticalement un capillaire, par exemple un tube en verre constitué d’un tube central ouvert aux deux extrémités et de diamètre petit, de l’ordre du mm.  On observe une montée de l’eau à l’intérieur du tube capillaire (Fig. 4.4).

Figure 4.4.  Situations comparées de molécules à l’intérieur ou à l'extérieur du tube capillaire.

S’il y a dénivellation c’est que la pression P₁ à l’intérieur du capillaire est différente de la pression P₁'.  Sur le plan déterminé par le segment MN sur cette figure 4.4, on peut écrire la relation suivante :

4.1                                          P₁'  =  P₁  ± (d₁ – d₂) h g

Dans cette relation, d₁ et d₂ sont respectivement la densité du liquide et celle de l’air, h est la hauteur de colonne d’eau dans le capillaire et g l’accélération de la pesanteur.  Dans le cas de l’eau, on observe que P₁'  >  P₁.  On observe une montée capillaire.  Par contre, dans le cas du mercure on observe une descente capillaire.  Ces observations justifient la présence du signe ± dans la formule 4.1.  Dans cette relation,

Cette différence de comportement est liée à la présence de la tension de surface, tension qui peut être positive ou négative.  Elle est déterminée par la loi de JURIN.  Examinons la figure 4.5 et, plus spécialement, l’intérieur du capillaire :

Figure 4.5.  Montée capillarimétrique.

Un examen fin de la surface du liquide (de l’eau par exemple) montre que cette surface normalement plane se termine sur les bords du capillaire par une remontée du liquide sur les parois du capillaire, ce qui se traduit par un rayon de courbure.  Dans le cas général, cette courbure ne se termine pas de manière tangentielle avec les parois du capillaire de telle sorte que l’on observe un angle q entre la surface du liquide et le point de contact supérieur du liquide. 

La dénivellation de la colonne de liquide est le résultat d’un compromis entre d’une part une force ascensionnelle due à la tension de surface et d’autre part à une force contraire liée à la masse de la colonne d’eau.  La force ascensionnelle est donnée par la relation suivante :

F_asc  =  2 p r s cos q

La force liée à la pesanteur s’exprime par une relation bien connue :

F_desc  =   p r² h g (d₁ – d₂)     ou encore    F_desc  =   p r² h g d   avec d₁ >> d₂

À l’équilibre ces deux forces sont égales et de sens contraire de telle sorte que :

F_desc  =   F_desc 

2 p r s cos q    =   p r² h g d   

Dans le cas de l’eau, l’angle de contact q est nul, de telle sorte que cos q = 1 et donc,

4.2                                           s  =  (1/2) h d g r

Dans cette formule s est la tension superficielle (exprimée en dyne/cm dans le système CGS), h est la hauteur de la montée (de la descente) capillarimétrique, d est la densité du liquide, g est l’accélération de la pesanteur et r est le rayon interne du capillaire

Pour des mesures de précision, il faut apporter deux corrections à la formule 4.2. La première concerne la densité du liquide d_l.  Il faut tenir compte de la densité de l’air d_air, plus généralement  du gaz en équilibre sur le liquide.  Ensuite, la hauteur h doit tenir compte du ménisque.  Ces deux corrections entraînent que la relation 4.2 devient

4.2a                        s  =  (1/2) (h + r/3) (d_l – d_air) g r

c.       La méthode de la goutte pendante

Il existe plusieurs méthodes de mesure de la tension de surface.  Par exemple, considérons un capillaire contenant un liquide.  Si on laisse le liquide s’écouler lentement, il se forme des gouttes de liquide qui se détachent successivement.  Tout se passe comme si sous l’effet de la tension de surface le liquide formait une sorte de « sac » qui emprisonne les molécules de liquide.  Lorsque la masse de la goutte dépasse une certaine valeur ce sac se rompt et la goutte tombe.  Cette rupture survient lorsque les forces liées à la pesanteur sont égales aux forces liées à la tension de surface (Fig. 4.6).

Figure 4.6.  La méthode de la goutte pendante.

Comme on n’a pas nécessairement accès à la masse de la goutte au moment de la rupture, on montre qu’il existe une relation entre cette masse et le diamètre de la goutte.

d.      La stalagmométrie

C’est une méthode utilisée par les pharmaciens puisqu’elle se rapporte au dosage des gouttes.  Elle est dérivée de la précédente.  Au lieu de mesurer le diamètre de la goutte, on mesure le nombre de gouttes qu’il faut pour obtenir un certain volume de liquide.  À travers la densité du liquide, on obtient donc facilement la masse de chaque goutte.

e.       La méthode de traction d’une lame verticale

Cette méthode est différente des précédentes.  On installe sur une extrémité d’un fléau de balance une lame métallique dont on connaît la masse.  Une fois l’équilibre atteint, la lame étant hors du liquide, à l’aide d’une vis sans fin on remonte lentement un bac chargé du liquide.  Au moment où il y a contact entre la lame et le liquide, une force d’attraction se développe et la lame plonge dans le liquide. On doit alors augmenter la pesée sur l’autre plateau de la balance pour ramener le fléau à sa position d’équilibre.  La différence de masse entre ces deux masses donne accès à la mesure de la tension de surface du liquide.

Figure 4.7.  La méthode de traction sur une lame.

f.        La méthode d’arrachement (tensiomètre de LECOMTE DU NOÜY)

La méthode ressemble beaucoup à la précédente.  On remplace la lame précédente par un anneau en platine très bien calibré et évidemment très propre.  Par contre, cette fois on immerge l’anneau dans le liquide.  On positionne le fléau de la balance à l’équilibre (Fig. 4.8).  Avec la vis sans fin on abaisse lentement le réservoir de liquide.  Au moment où l’anneau tend à sortir du liquide, la tension de surface se développe : l’anneau est attiré vers le liquide et suit le mouvement descendant du niveau de liquide.  Il faut alors continuellement ajouter des poids sur l’autre plateau de la balance pour le maintenir en position horizontale…  jusqu’au moment où l’on observe la rupture des forces. 

Au lieu d’un plateau de balance qui ne permet pas un contrôle fin de la pesée, l’appareil est constitué d’un disque gradué qui permet une lecture directe de la tension. L’appareil est muni d’une sorte de vernier qui permet une lecture fine de la tension.  La figure 4.9 permet de visionner ce que l’on observera lorsque le fléau du tensiomètre tire l’anneau vers le haut : le liquide demeure en quel que sorte coller à l’anneau.

Figure 4.8.  Schémas du tensiomètre de LECOMPTE DE NOUY.
B : butées du fléau ; V : vis sans fin permettant le déplacement vertical de l’échantillon ;
M : système de vernier pour une lecture fine de la tension.

Figure 4.9.  Effet de la montée de l’anneau sur la surface du liquide.

g.       La tension de surface et l’effet de la température

La tension de surface d’un liquide diminue avec l’augmentation de la température.  On peut même prévoir, compte tenu des propriétés du point critique que la tension de surface doit être nulle à la température critique du liquide.  Le tableau 4.4 donne quelques valeurs de cette tension de surface.  On notera que toutes ces valeurs sont exprimées dans le système CGS.  Cela tient essentiellement à deux raisons.  La première est que beaucoup de mesures ont été faites avant que le SI obtiennent ses lettres de noblesse et de plus les grandeurs des tensions de surface s’expriment avec des nombres tout à fait compatibles en grandeurs avec les valeurs des unités de ce système.

Tableau 4.4.  Tension* de surface de quelques liquides

Ce tableau montre un détail intéressant en ce qui concerne l’eau : sa tension superficielle est nettement supérieure à celle des autres constituants.  La structure de la molécule qui comprend un moment dipolaire élevé entraîne des interactions molécules relativement fortes (liaisons de VAN DER WAALS).  Ces interactions intermoléculaires entraînent l’existence d’une tension superficielle forte.

Il existe un certain nombre de relations empiriques qui indiquent la variation de la tension de surface s en fonction de la température (note : Tc est la température critique).

4.3                                          s  =  s₀ ( 1 – T_R)^11/9      où   T_R  =  T / Tc

s₀ est une caractéristique du liquide considéré.  Le tableau 4.5 donne quelques valeurs de s et de s₀  pour quelques liquides.

Tableau 4.5.  Valeurs caractéristiques de la tension de surface* de quelques liquides

Une autre formule est celle RAMSAY-SHIELDS : elle est valide tant et aussi longtemps que la température du liquide est inférieure de 30 º à la température critique.

M est la masse molaire et d_l la densité du liquide.  Le premier membre de l’équation 4.4 est appelé l’énergie molaire de surface.  Notons que la tension de surface devient nulle lorsque :

T =  Tc – 6.

Cette formule a été corrigée par KATAYAMA : 

Dans cette équation, d_v est la densité de la phase vapeur.  Cette équation satisfait la remarque faite plus haut : la tension de vapeur devient nulle à la température critique.

            h- La composition d’un savon

Bien évidemment la tension de surface est une propriété importante lorsqu’on parle de lavage.  Ainsi une poudre à laver le linge doit être en mesure d’abaisser la tension de surface de l’eau de manière à faciliter le lavage par dissolution des impuretés à enlever.  En fait, la composition de ces poudres est maintenant complexe.  On trouvera une description simplifiée de cette composition simplifiée à l'annexe située en fin de ce chapitre.

2.3.            La viscosité

1. Hypothèse de NEWTON

Supposons deux plans d’un liquide se déplacent à des vitesses différentes : le premier se déplace avec une vitesse v et le second avec une vitesse v + dv (Fig. 4.10).  Supposons aussi que ces deux plans sont situés à une distance ds l’un de l’autre.  Le rapport  dv / ds est appelé le gradient de vitesse, ou encore la variation de vitesse par unité de distance.

Figure 4.10.  La viscosité : hypothèse de NEWTON.

En glissant l’un sur l’autre, il se produit une friction entre ces deux plans : ce sont des forces de friction interne.  Le glissement d’un tel plan sur les parois du conduit produit des forces de friction externe.  La force de friction d’un plan sur un autre, encore appelée la force de cisaillement, t, est donnée par la relation :

4.6                                                                                     t  =  Q ( dv / ds ) h

La force de friction interne est proportionnelle à la surface de contact Q entre les deux plans.  Elle est aussi proportionnelle au gradient de vitesse ainsi qu’à la viscosité du fluide h.  Ce facteur peut être perçu comme la force, par unité de surface, nécessaire pour faire glisser un plan du fluide sur un autre situé à une distance unitaire et à une vitesse unitaire par unité de temps. Le rapport t  / Q est appelé la force de cisaillement par unité de surface.

Dans le cas d’un gaz idéal, la théorie cinétique des gaz montre que le coefficient de viscosité est relié à la densité du gaz d, à son libre parcours moyen l ainsi qu’à la vitesse moyenne des molécules :

En introduisant la valeur de la vitesse moyenne des molécules, vitesse obtenue via la théorie cinétique des gaz équation 2.27, on obtient :

  Il est intéressant de constater que la mesure du coefficient de viscosité permet d’atteindre à travers des paramètres très accessibles, le libre parcours moyen des molécules dans le fluide gazeux.  Par ricochet, la mesure du libre parcours moyen permet d’accéder au diamètre moléculaire : voir l’équation 2.30.

    b.   Effet de la température

À une augmentation de la température correspond une augmentation de volume du liquide.  Les molécules s’éloignant les unes des autres, les interactions intermoléculaires s’affaiblissent avec l’augmentation de la température.  On peut donc s’attendre à une diminution de la viscosité avec une telle augmentation.

Figure 4.11.  Effet de la température sur la viscosité de quelques liquides.

Plusieurs équations empiriques ont été proposées pour traduire la variation de la viscosité en fonction de la température.  Une formule simple est la suivante :

log   = A / T  +  B

A et B sont des constantes caractéristiques de chaque liquide et T est la température exprimée en kelvin.

Un cas particulier de la variation de la viscosité avec la température est celui du soufre liquide.  Au-dessus de 120 °C le soufre est liquide et sa viscosité diminue avec une augmentation de la température.  Vers 155 °C, la viscosité atteint une valeur minimum et, avec une élévation de température, on observe une remontée rapide de la viscosité qui atteint son maximum vers 200 °C.  Au-delà de 200 °C, la viscosité redescend avec l’augmentation de la température (Fig. 4.12).  Cette brutale augmentation de la viscosité du soufre liquide traduit la modification moléculaire du soufre.  Constitué de molécules cycliques S₈ en dessous de 160 °C, les cycles s’ouvrent et forment des chaînes qui se recombinent pour former de très longues chaîne S_n.  Au-dessus de 400 °C, les longues chaînes se rompent et  en forment de petites : S₈,  S₆  et S₂.  Au-dessus de 1700 °C, il ne reste plus que des molécules S₂ en phase gazeuse.

Figure 4.12.  Effet de la température sur la viscosité du soufre liquide.

    c.   Effet de la température sur la viscosité des gaz

Il est intéressant ici de présenter l’effet de la température sur la viscosité des gaz.  En effet, contrairement à ce que l’on vient de voir pour les liquides, la viscosité des gaz croît avec l’augmentation de la température (Fig. 4.13).  La tendance observée pour l’air l’est aussi pour de nombreux gaz.

Figure 4.13.  Effet de la température sur la viscosité de l’air.

La viscosité des gaz est toujours reliée aux interactions intermoléculaires comme dans les liquides.  Par contre, ces interactions dépendent moins de la distance intermoléculaire que de l’importance des collisions.  On peut traduire ceci en disant qu’en phase gazeuse, aux pressions ordinaires, les molécules sont tellement éloignées les unes les autres que les interactions intermoléculaires sont négligeables sauf au moment où surviennent les collisions.  Or le nombre de collisions par seconde, la vitesse de collision, est une fonction de la température, plus précisément il dépend de la racine carrée de la température.  Il devrait donc en être ainsi de la viscosité.  C’est ce que montre la figure 4.14.

Figure 4.14.  Effet de la racine carrée de la température sur la viscosité de l’air.

4. L’effet de la pression sur l’écoulement d’un liquide

L’écoulement d’un liquide dans un conduit est intuitivement fonction de la pression qui lui est appliquée.  En d’autres termes la vitesse d’écoulement d’un liquide est dépend directement de la pression à laquelle il est soumis.  Cette affirmation est traduite par la loi de NEWTON :

4.8                                k P  =  h v    Þ      v  =  k P / h

P est la pression appliquée au liquide ; v est la vitesse d’écoulement ; h est la viscosité du liquide et k une constante de proportionnalité. Si la relation 4.8 se vérifie, on dira que les liquides sont newtoniens.  C’est ce que l’on observe lorsque les molécules sont sphériques.  Si la loi ne tient pas, on dira que le liquide est non newtoniens.  C’est le cas des molécules qui ne sont pas sphériques, par exemple en forme de bâtonnets.

La viscosité h est donnée par l’équation développée par POISEUILLE :

V est le volume de liquide qui passe pendant un temps t dans un capillaire de rayon r et de longueur l; P est la pression appliquée à la tête du capillaire.  Notons que le rapport V/t correspond à un débit ou encore à la vitesse d’écoulement du liquide.  Cette expression 4.9 est donc bien équivalente à 4.8.  Si l’on mesure le temps nécessaire pour l’écoulement du même volume de deux liquides différents, on obtient :

e.       La mesure de la viscosité

Dans le cas d’un capillaire vertical, la pression exercée sur le liquide est celle de sa propre masse :

P =  m g h  Þ  P  =  V d g h  ou encore P, le poids, est proportionnel à la densité d.

Par conséquent en connaissant les densités de deux liquides ainsi que les temps de passage dans un capillaire, la connaissance de la viscosité du liquide 1 permet de connaître la viscosité du liquide 2.  Cette observation est mise à profit à l’aide du viscosimètre d’OSWALD (Fig. 4.15).

Figure 4.15.  Schéma du viscosimètre d’OSWALD.

Le principe de fonctionnement est fort simple.  On remplit le réservoir qui se trouve au-dessus du capillaire.  Le liquide est soumis à la seule force de l’accélération de la pesanteur.  On mesure le temps d’écoulement en repérant le passage de la surface du liquide entre les repères x et y (Fig. 4.15). 

Note : l’écoulement du liquide dans le tube capillaire doit être lamellaire et non pas turbulent.  Un cours de mécanique des fluides approprié montre que telle est la situation lorsque le nombre de REYNOLDS, R,  est inférieur à 2000.  Ce nombre de REYNOLDS, sans dimension, est donné par la relation :

4.12                                                 R  =  v d D / h

En plus de la vitesse d’écoulement v, de la densité d et de la viscosité h du liquide, ce nombre R dépend du diamètre D du capillaire.

Une deuxième méthode très employée utilise le viscosimètre d'UBBELHODE.  Cette méthode est encore appelée la méthode de la bille tombante.  Cette fois on mesure non pas le déplacement du liquide mais plutôt le déplacement d’une bille métallique dans un liquide sous l’effet de l’accélération de la pesanteur.  En fait la bille atteint rapidement une vitesse limite uniforme lorsque les forces de pesanteur sont égales aux forces de friction.  Une sphère de rayon r et de densité d traverse un milieu fluide de densité d_m  sous les forces de la gravité est soumise à la force suivante :

F_grav =  4/3 p r³ (d  -  d_m) g

La loi de STOKES établit la force due à la friction, à la viscosité du milieu :

F_visc =  6 p r h v

La vitesse limite est atteinte lorsque ces deux forces sont égales :

4/3 p r3 (d  -  d_m) g  =  6 p r h v _lim

Cette relation est connue sous le nom de loi de STOKES.  Elle est applicable à un corps sphérique pourvu que le diamètre de cette sphère soit beaucoup plus grand que la distance entre les molécules du fluide.  Comme dans le cas de l’utilisation du viscosimètre d’UBBELHODE, ce type de viscosimètre s’accommode bien de la méthode de comparaison entre deux fluides.  Il serait facile de montrer que :

Un terme fréquemment employé dans ce domaine est celui de la fluidité f.  Elle se définit comme étant l’inverse de la viscosité :

f        =  1  / h .

Le tableau 4.6 montre quelques valeurs de la viscosité de liquides.

Tableau 4.6.  Viscosité* de quelques liquides en fonction de la température (°C)

Il est intéressant de remarquer que la viscosité de l’eau pure est voisine de 1 centipoise à 20 °C, tout comme la densité de l’eau est aussi voisine de l’unité dans le système CGS.  On utilise la notion de viscosité relative h_r ( notion à ne pas confondre avec une notion similaire introduite dans le cas des solutions : voir plus bas) en utilisant cette propriété.  En effet à partir de la relation 4.14, on obtient :

h_r  =  0,01 d₁ t₁ / t₂

Dans cette dernière relation, h_r est la viscosité relative d'un liquide exprimée en poises.

f.        Les unités

Dans le système international d’unités SI, on définit la viscosité « dynamique », la viscosité dont il a été fait état jusqu’à maintenant dans ce chapitre.  Elle s’exprime en pascal · seconde : c’est la viscosité d’un liquide sur lequel il faut appliquer une force de 1 N · m^-2 pour obtenir une différence de 1 m/s entre deux surfaces distantes de 1 m.  Le pascal · seconde est parfois appelé le poiseuille.  L’équivalent dans le système CGS est le décapoise.

Il existe aussi la viscosité « cinématique » définit dans le système MKSA qui a précédé le SI, par le myriastokes.  La viscosité cinématique hc d’un fluide dont la viscosité dynamique est de 1 pascal · seconde  et la masse volumique est de 1 kg / m³ :

h_c  =  h/d   ou encore h  =  hc d  

Elle s’exprime donc en m²/s :

[hc]  =  [h]/[d]  =    pascal · seconde / (kg / m³)  =

[hc]  =  (N m^-2) s m³ / kg   =  (kg m s^-2  m^-2) s m³ / kg

[hc]  =   m² / s     C.Q.F.D.

Avec un liquide de référence x, on a aussi :

g.       Le cas des solutions

En effet, si dans un solvant courant comme le méthanol on introduit un soluté, Les molécules de celui-ci vont jouer un rôle important dans les forces de friction qui se développent lorsque le solvant est en écoulement.  Une solution aqueuse saline a une viscosité dynamique différente de celle de l’eau pure : les molécules d’eau solvatées autour d’un ion positif forment des grappes de molécules bien différentes de celles que l’on peut retrouver dans l’eau pure.  La viscosité est donc altérée par ces solutés.

On définit la viscosité relative h_r d’une solution comme étant le rapport de la viscosité de la solution h sur celle du solvant pur h₀ (ne pas confondre avec une notion similaire introduite plus haut).

4.15                                        h_r  =  h/h0

On définit également la viscosité spécifique h_s comme :  h_s  =  h_r    - 1.

Ou encore :

Enfin, on définit la viscosité intrinsèque [h] de la solution la limite lorsque la concentration du soluté (le polymère) tend vers zéro du rapport de la viscosité spécifique h_s de la solution sur la concentration C :

Note : la IUPAC recommande l’appellation « nombre de viscosité limite » pour [h].

La figure 4.16 montre l’exemple du polychlorure de vinyle dans le cyclohexane à 25 °C.  On porte en fonction de la concentration C du polymère, ici exprimée en grammes par 100 cm³ de solvant, le rapport  hs /C.  En extrapolant cette courbe vers la concentration nulle, on obtient la valeur de la viscosité intrinsèque.

Figure 4.16.  Variations de diverses fonctions liées à la viscosité avec la concentration du polychlorure de vinyle dissout dans la cyclohexanone à 25 °C.

On montre aussi que la limite lorsque la concentration du soluté (le polymère) tend vers zéro du rapport de la viscosité relative h_r de la solution sur la concentration C (Fig. 4.14) :

Ce qui vient d’être dit d’une solution peut donc être appliqué au cas des solutions de polymères.  La viscosité est une propriété qui a été et est utilisée pour déterminer certaines propriétés des macromolécules ou des polymères.  Le changement de la masse des polymères, donc le changement de la grosseur des macromolécules, doit affecter les mesures de viscosité.  STAUDINGER (1932) a proposé que la viscosité intrinsèque d’une solution de polymère soit une fonction de la masse de ce dernier :

[h]  =  k  M

Plus généralement on observe que :

[h]  =  k  Ma

ou encore :

Ln [h]  =  a Ln  M + constante

Les valeurs de k et de dépendent du couple solvant – polymère.  Ce sont donc des caractéristiques des interactions entre les molécules de solvant et de polymère.  Par exemple, on observe que lorsque les molécules de polymères ressemblent à des assemblages du type «ressort» flexible ou de simples hélices, le coefficient a est voisin de 2.  Par contre si le polymère est formé de sphères rigides, ce même coefficient tend vers zéro.

3. Les propriétés thermiques

3.1       La mesure de la température d’ébullition

     a.  La relation pression - température d'ébullition

La température du point d’ébullition T_e (ou le point d’ébullition) est une fonction de la pression :  T_e  =  f(P).  Cette relation est explicitée à travers la relation de CLAPEYRON :

L₁₂ est la chaleur latente de transformation du composé passant de la phase 1 à la phase 2, ici de la phase liquide à la phase gazeuse.  Le mot « latente » signifie que la transformation s’opère sans changement de température.  Le lecteur est maintenant familier avec les notations molaires qui sont surmontées d’un trait horizontal.  Dans le cas de l’ébullition, le volume molaire d’une quantité quelconque du gaz est beaucoup plus grand que celui de la phase gazeuse.  On peut donc négliger le premier devant le second :

En intégrant cette équation on obtient :

4.19

Cette intégration n’est valide que si la chaleur latente de changement de phase demeure constante.  Cela est vrai sur une échelle de température relativement restreinte : quelques dizaines de degrés tout au plus.  Si l’intégration est effectuée sur un intervalle de température plus large, on utilise des formules dont un très connue applicable à la vaporisation de l’eau :

Cette relation est connue sous le nom de la loi de KIRCHHOFF-RANKINE.  Une formule également très largement utilisée est la loi d’ANTOINE.  C’est une formule en quelque sorte simplifiée de la précédente :

La pression P est exprimée en bar et les coefficients A, B et C sont des valeurs empiriques.  Les formules sont données avec les plages de températures où elles sont applicables (Tableau 4.7).

Tableau 4.7.  Valeurs de quelques coefficients de l’équation d’ANTOINE

En résumé : puisque la température d’ébullition dépend de la pression, la pression doit toujours être fixée pour mesurer le point d’ébullition.  Il est intéressant de noter qu’à l’altitude de 3800-3900 m, l’altitude de La Paz, Bolivie, l’eau bout vers 83 °C.  Il en résulte que le temps de cuisson à l’eau des aliments est plus long qu’au niveau de la mer.  Inversement, l’augmentation de la pression à deux bars entraîne une augmentation de 20 °C de la température d’ébullition.

       b.   La relation point d’ébullition – structure des molécules

Il est intéressant de connaître, s’il en existe, les relations qui existent entre le point d’ébullition et la structure des molécules.  Par exemple, on peut présumer que plus la chaleur latente de vaporisation (l’enthalpie de vaporisation DH_vap) est élevée et plus la température d’ébullition est aussi élevée.  C’est la règle de PICTET-TROUTON:

DHvap  =  a T_e

Le coefficient a est une constante qui est égale à 83 pour beaucoup de composés dont les hydrocarbures et à 108 pour les alcools lorsque la température est exprimée en kelvin et la chaleur latente de vaporisation est exprimée en J/mol.  Originellement, la loi était exprimée en kelvin/(kcal/mol).

Dans le cas des hydrocarbures, la formulation de NEKRASSOW tient compte de la complexité structurale de la molécule.  Il attribue à un atome ou à un groupe d’atomes un incrément e qui est introduit dans la formulation.  Ainsi plus la molécule contient d’atomes ou groupes d’atomes et plus la somme des incréments Se est importante :

M est la masse moléculaire de l’hydrocarbure.  Le tableau 4.8 donne un aperçu des incréments pour un hydrocarbure plus ou moins saturés.

Tableau 4.8.  Incréments relatifs à la formule de NEKRASSOW

Il existe aussi une règle et un tableau de valeurs d’incréments correspondant pour les composés polaires.

3.2.      La mesure de la température de congélation

La congélation désigne bien sûr le passage de la phase liquide vers la phase solide, le chemin inverse étant bien entendu le processus de fusion.  La  loi de CLAPEYRON est encore valide :

Cette fois le volume du solide est voisin de celui du solide.  On ne peut plus ignorer l’un devant l’autre.  De plus puisque la différence entre ces deux valeurs est petite le membre de gauche de cette équation est très grand.  Il s’ensuite que les tangentes à la courbe P = f(T) sont très fortement inclinées, voire proche de la verticale.  La courbe P = f(T) est donc pratiquement verticale, en tout cas beaucoup plus que ne l’était la courbe de vaporisation (Fig. 4.17).

Par exemple, dans le cas de la fusion de la glace, l’augmentation de la pression d’une atmosphère entraîne une diminution de la température de fusion de 0,0075 °C, une variation de température difficilement mesurable avec un thermomètre gradué au dixième de degrés.  Cet écart de température est également négligeable devant la variation observée de la température d’ébullition avec l’augmentation de la pression.

Figure 4.17.  Courbes de fusion et courbe de vaporisation.

Par conséquent si le volume molaire du liquide est plus grand que celui du solide, la pente est positive : c’est le cas général.  Par contre, si c’est l’inverse, la pente est négative : c’est le cas de l’eau et du bismuth.  Il est bien connu que la glace flotte sur l’eau.  La figure 4.17 correspond donc à ce cas.

Note 1 : Puisque la température de fusion est peu affectée par la variation de pression, il n’est pas important de préciser la température à laquelle la mesure a été effectuée ; contrairement à ce qui a été dit dans la cas de la température d’ébullition.

Note 2 : Puisque le volume du gaz est toujours plus grand que le volume du liquide, la tangente à  la courbe de vaporisation ou d’ébullition est toujours positive : la température d’ébullition croît avec la température.

Il est intéressant de noter que si l’on met de l’eau dans un récipient, par exemple un calorimètre, et qu’on mesure la température de l’eau pendant le processus de refroidissement, on constate que la température demeure constante tant et aussi longtemps que la solidification n’est pas complétée.  On montrera dans le cours de thermodynamique chimique (Chapitre 7.2) que durant le processus de changement de phase d’un constituant pur, la température du changement de phase est invariante.  La même observation peut donc être faite pendant le processus de liquéfaction (le passage de l’état vapeur à l’état liquide. 

Si l’on enregistre la température de l’échantillon en fonction du temps, on obtient une courbe telle que celle présentée à la figure 4.18.  Les paliers de changement de phase y apparaissent clairement.

Figure 4.18.  Courbe de refroidissement de la vapeur d’eau.

3.3.      La mesure de la température de sublimation

À nouveau la loi de Clapeyron est encore valide :

Également, le volume molaire du gaz est beaucoup plus grand que celui du solide.  Par conséquent, le volume du solide peut être ignoré devant celui du gaz :

Tout comme dans le cas de la vaporisation, on montre que :

avec les remarques similaires.  La figure 4.19 montre la courbe de sublimation d’un corps pur.

  Figure 4.19.  Courbes de sublimation.

3.4.      La mesure du point triple

La courbe de vaporisation est le lieu géométrique des points (P,T) où il y a coexistence des phases liquide et gazeuse.  De même, la courbe de fusion correspond au lieu géométrique des points (P,T) où coexistent les phases solides et liquide.  Au point de concours de ces deux courbes, on a donc coexistence des phases solide, liquide et gazeuse.  Ce point d’intersection des deux courbes de fusion et de vaporisation appartient donc aussi à la courbe de sublimation puisqu’il y a équilibre entre les phases solide et gazeuse.  On appelle ce point (P,T) le point triple.  On montre par la règle de la variance que ce point est caractéristique de la substance. Il est de plus unique en ce sens que c’est le seul point (P,T) où l’on peut observer la coexistence de ces trois phases solide, liquide et gazeuse  (Fig. 4.20).

Figure 4.20.  Le point triple.

Au point de concours des courbes de sublimation et de vaporisation, l’application de loi de CLAPEYRON permet d’écrire :

Puisque les volumes molaires des solides et des liquides sont beaucoup plus petits que celui des gaz,

Au point triple, l’enthalpie de sublimation est plus importante que celle de la vaporisation.  En effet, la sublimation est en quelque sorte la somme de deux processus : la fusion et la vaporisation.  L’enthalpie de sublimation est donc égale à la somme des enthalpies de fusion et de vaporisation  (Fig. 4.20) :

puisque

on peut conclure que la tangente à la courbe de sublimation au point triple (angle a sur la figure 4.20) est supérieure à celle à la courbe de vaporisation en même point triple (angle a' sur la même figure) :

angle a  >  angle a'  

Figure 4.21.  Les énergies de changement de phases au point triple.

Tableau 4.9.  Propriétés de quelques points triples

Il faut noter que la courbe de fusion étant pratiquement verticale sur le diagramme montrant la pression en fonction de la température, il s’ensuit que la température du point triple est voisine de la température de fusion du même composé sous la pression atmosphérique.  On peut même ajouter que la température du point triple est généralement inférieure à la température de fusion puisque la courbe de fusion a généralement une pente positive (Tableau 4.9).  Ce n’est évidemment pas le cas de l’eau puisque la courbe de fusion a une pente négative.

3.5.            Description de l’état liquide

Le tableau 4.10 donne les chaleurs de changement de phases de quelques molécules de même que le rapport des énergies de fusion relativement à celle de la vaporisation.  On remarque que l’enthalpie de vaporisation est beaucoup plus grande que celle de la fusion.  Cette dernière est en général 10 % de la précédente.  Par conséquent, la phase liquide est beaucoup plus proche de la phase solide que de la phase gazeuse puisque le système demande beaucoup plus d’énergie pour sa vaporisation que pour sa fusion.  Les distances intermoléculaires en phases condensées sont similaires : les interactions son grandes entre les molécules.  Ce n’est plus le cas en phase gazeuse.  On l’a vu dans les chapitres précédents : à la limite (dans le cas du gaz idéal) il n’y a plus d’interactions entre les molécules dans la phase gazeuse.

Tableau 4.10.  Comparaison entre les chaleurs latentes de changement de phase* pour quelques composés

M				M
A	1,17	7,86	0,15	Na	2,63	11,0	0,024
H2	0,117	0,92	0,13	Al	10,66	282,6	0,038
O2	0,40	9,69	0,05	Ag	11,29	290,1	0,039
N2	0,91	7,06	0,13	Hg	2,42	64,8	0,037
CO	0,84	7,94	0,11	Mn	14,41	291,3	0,050
CH4	0,94	8,17	0,115	Tl	3,18	179,7	0,018
CCl4	2,69	29,82	0,09	NaF	32,65	890	0,037
CH3OH	2,196	35,21	0,062	KCl	26,8	690	0,039
H2O	5,97	47,23	0,13	KBr	16,1	665	0,018
CO2	8,32	26,92	0,31	* : en kJ/mol.

4. Conclusions  

Pour en savoir plus

Maron, S. H. et C. F. Prutton, Principles of Physical Chemistry, 4^e Édition, The MacMillan Company, New York, 1965.

Le Handbook of chemistry and physics, CRC Press, contient une grande variété et quantité d’informations très utile au chimiste.  Ainsi, on trouve dans la 70^e édition, 1989-1990, les tables suivantes :

Sur la formulation des poudres à laver :

Les lessives en poudre – Un siècle d’innovations pour éliminer les taches,  Nardello-Rataj, V., L. Ho Tan Taï et J.-M. Aubry, L’actualité chimique, Soc. française de chimie, 3-10, mars 2003.

Liens utiles :

NOTE:

Le recours au WWW (World Wide Web) pour trouver l'information recherchée et devenu maintenant courant et surtout facile. Outre le fait que la pérennité des sites web est loin d'être assurée, ils n'ont pas tous le même degré de fiabilité. Il faut donc user de sens critique.  Les sites gouvernementaux ou para gouvernementaux (ceux des universités, par exemple), ceux des grandes corporations industrielles, ceux des Fondations, ... sont parmi les plus sûrs et donc recommandables.

On trouvera des valeurs de points triples ainsi que les coefficients de l’équation d’ANTOINE pour un grand un grand nombre de produits chimiques dans un site de la Société américaine de chimie (site en anglais et accessible gratuitement) à l’adresse suivante :

https://webbook.nist.gov/chemistry/ (visité le 2019-02-12).

Ce site contient également des données thermodynamiques sur les changements de phase, les spectres infrarouges, ultraviolet, de masse,… et plusieurs autres données physiques dont les température de fusion, d’ébullition, critique, …

De nombreuses informations et des biographies sont accessibles dans le Dictionnaire interactif des sciences et techniques.  Il faut s'inscrire et le site n'est pas gratuit. Cliquez sur http://www.sciences-en-ligne.com/comm/ et aussi ailleurs.

Une application amusante de la densité se retrouve dans ce qui est appelé le thermomètre de GALILÉE.  En plus de son historique, on en en trouvera une descrition et son principe de fonctionnement sur le site de Wikipedia.

Et aussi les biographies de POISEUILLE, STOKES, RAMSAY,  RANKINE, REYNOLDS, ...

Annexe

La composition d’une poudre à laver

Le consommateur, de manière consciente ou inconsciente et probablement en partie conditionné par une publicité agressive, s’attend à ce que la poudre à laver le linge ou la vaisselle réalise plusieurs objectifs.  Non seulement cette poudre doit elle être facile à utilisée,  elle doit enlever la saleté, mais encore redonner de l’éclat ainsi que la souplesse au linge, éventuellement restaurer l’odeur du neuf et bien sûr ne pas laisser de dépôts visibles ou nuisibles.  La poudre doit aussi ne pas s’attaquer aux fibres naturelles ou synthétiques du linge et minimiser ses interactions avec l’environnement.  L’usage de tissus demandant des températures douces au lavage ont conditionné l’apparition de produits relativement performants.  Dans le détail, une poudre à laver peut contenir plusieurs des additifs qu’on peut classer en deux catégories : les additifs actifs et les auxiliaires de formulation.

i-                    Les additifs actifs

On trouve bien sûr les agents tensioactifs dont l’objectif est d’abaisser la tension inter faciale et de faciliter le mouillage des fibres.  Ils doivent aussi décoller les salissures et les maintenir dans le bain.  Les molécules les plus utilisées sont des alkylbenzène sulfonates de sodium (Tableau 4.11).  Les chaînes alkyles sont linéaires pour assurer une meilleure biodégradabilité et pour éviter la formation de mousse dans les rivières.  Ils sont cependant sensibles aux ions alcalino-terreux : ils peuvent précipiter.  On leur ajoute des acides gras naturels à chaîne longue, C₁₆ à C₂₂, qui ont des propriétés complexantes vis à vis des ions alcalino-terreux et donc préviennent la précipitation des agents tensioactifs

Suit le perborate de sodium qui décolore les tâches par oxydation auquel on ajoute un activateur du perborate, le tétraacétyléthylènediamine.

L’ajout d’enzymes favorise la dégradation de salissures d’origine biologiques.  Finalement, on ajoute des agents azurant.  Ces molécules absorbent la lumière dans le proche ultraviolet et réémettent dans la région du bleu.  Elles ajoutent au linge « l’éclat à la blancheur » selon une publicité bien connue en Europe francophone.

Tableau 4.11.  Exemple de formulation d’une poudre à laver : produits actifs

Nom	Formule	Pourcentage
alkylbenzène sulfonates de sodium	*	10 – 20
perborate de sodium		12 – 18
tétraacétyléthylènediamine		5 – 8
enzymes	Lipase, protéase, amylase, . . .	1 – 2
agent azurant		0 – 1
	* Note : x + y = 9 à 15.

  La liste de ces produits est plus ou moins longue.  On trouve les acides gras saturés à longue chaîne mentionnés plus haut : ils jouent le rôle de  produits anti moussants. Pour lavage avec des eaux très dures, on utilise des anticalcaires.  Ce sont le plus souvent des zéolithes.  Des copolymères des acides maléique et acrylique renforcent l’action anticalcaire.  L’ajout d’alcalinisant comme le disilicate de calcium renforce l’action des zéolithes et constitue un inhibiteur de corrosion.  Le carboxyméthylcellulose de sodium empêche la redéposition des salissures du bain de lessive sur le linge.  L’ajout de molécules parfumantes donne une odeur agréable au linge…  Pour assurer la cohésion des granules contenant tous ces additifs, on ajoute su sulfate de sodium (Tableau 4.12).

  Tableau 4.12.  Exemple de formulation d’une poudre à laver : produits auxiliaires

Nom	Formule	Pourcentage
Savon	CnH2n+1-COONa	0 - 1
Zéolithe	voir Fig. 10.22	15 - 20
Copolymère maléique et acrylique		4 – 6
Disilicate de sodium	Na2Si2O5	4 – 8
Carbonate de sodium	Na2CO3	12 -16
Carboxyméthylcellulose de sodium		0 - 1
Parfums	extraits d’huiles essentielles ou molécules de synthèse	0 - 1
Eau et sulfate de sodium	H2O,  Na2SO4	Qsp 100*
* Qsp 100 : quantité suffisante pour 100 %.

Tiré de Nardello-Rataj, V., L. Ho Tan Taï et J.-M. Aubry, L’actualité chimique, Soc. française de chimie, 3-10, mars 2003.

Problèmes

Problème Nº 1.  Utilisation du picnomètre

L’utilisation d’un picnomètre de volume voisin de 2 ml pour la mesure de la densité relative d’une huile essentielle indique les mesures de pesées suivantes obtenues à 21 °C :

      1-     picnomètre vide, m₀ : 6,066,  6,067 et 6,066 g
2-     picnomètre rempli d’eau distillée, m₁ : 8,201, 8,200 et 8,200 g
3-     picnomètre rempli d’huile essentielle, m₂ : 7,991,  7,990 et 7,990 g.

Calculez la densité relative de l’huile essentielle ainsi que l’incertitude absolue sur la valeur résultante.

    Réponse : d₂₁ = 0,902 ± 0,002

Problème Nº 2

Un liquide de masse volumique égale à 0,800 g/cm³ s’élève jusqu’à une hauteur de 62,5 mm dans un capillaire de 0,21 mm de diamètre.  Quelle est la tension superficielle de ce liquide ?  Estimer l’incertitude absolue sur ce résultat.

  Réponse : s  =  (25,72 ±  0,29) 10^-5 Newton/m

Problème Nº 3.  Descente capillarimétrique

Dans un tube de rayon 0,108 ± 0,004 mm, on observe une descente capillarimétrique de 6,60 ± 0,05 cm pour le mercure.  Calculez la tension de surface du mercure sachant que sa masse volumique est de 13,600 ±  0,005 g cm^-3.  Faire le calcul d’erreur pour déterminer la mesure qui entraîne la plus  grande incertitude, ainsi que l’incertitude expérimentale finale.

Réponse : s  =  475 ± 21  g s^-2  ou encore dyne/cm   

Problème Nº 4

a- En admettant que la tension de surface de l’eau est de 72 dyne/cm, calculez cette tension de surface dans le système SI.

b- Si la montée de la sève dans un arbre de 30 m est explicable sur la base de la montée capillarimétrique, quel devrait être le diamètre des canaux responsable de cette montée ?

Réponse :  r  =   0,49 mm    

Problème Nº 5

Une sphère en acier de 4,0 cm de diamètre et de 7,9  g cm^-3 de densité tombe de 1,00 m en 55 s dans l’huile de densité 1,1 g cm^-3.  Calculez la viscosité de l’huile en poises.